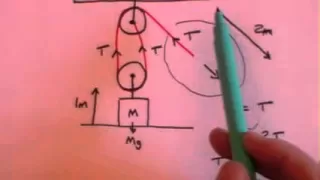
A review of pulleys, mechanical advantage, an inclined surface and gears. This is not part of the physics syllabus for many A level boards, but may be included in some Applied Maths courses.
From playlist Classical Mechanics

Simple Machines (1 of 7) Pulleys; Defining Forces, Distances and MA
For the pulley simple machine this video defines the terms input and output force, input and output distance and mechanical advantage. A simple machine is a mechanical device that changes the direction and the magnitude of a force. In general, they can be defined as the simplest mechanis
From playlist Mechanics

What is General Relativity? Lesson 58: Scalar Curvature Part 7: Pullback and Pushforward
What is General Relativity? Lesson 58: Scalar Curvature Part 7: Pullback and Pushforward This lecture covers the pullback of convector fields. Also, we cast pushforwards and pullbacks in terms of coordinate charts. Please consider supporting this channel via Patreon: https://www.patreon
From playlist What is General Relativity?

Simple Machines (2 of 7) Pulleys; Calculating Distances, Forces, MA, Part 1
For the pulley simple machine shows how to calculate the input and output distances, the input and output forces and mechanical advantage. A simple machine is a mechanical device that changes the direction and the magnitude of a force. In general, they can be defined as the simplest mech
From playlist Mechanics

Riemannian Geometry - Examples, pullback: Oxford Mathematics 4th Year Student Lecture
Riemannian Geometry is the study of curved spaces. It is a powerful tool for taking local information to deduce global results, with applications across diverse areas including topology, group theory, analysis, general relativity and string theory. In these two introductory lectures
From playlist Oxford Mathematics Student Lectures - Riemannian Geometry

Liouville's Theorem through Symplectic Geometry
Liouville's theorem in classical mechanics is almost immediate in its symplectic geometry incarnation. Here I describe why! In the previous video, I introduced Lie derivatives on vector fields, including a derivation that the symplecitc form is preserved under Hamiltonian flow: https://
From playlist Symplectic geometry and mechanics

Classical curves | Differential Geometry 1 | NJ Wildberger
The first lecture of a beginner's course on Differential Geometry! Given by Prof N J Wildberger of the School of Mathematics and Statistics at UNSW. Differential geometry is the application of calculus and analytic geometry to the study of curves and surfaces, and has numerous applications
From playlist Differential Geometry

Simple Machines (3 of 7) Pulleys; Calculating Forces, Distances, MA, Part 2
For the pulley simple machine shows how to calculate the input force, input distance and the mechanical advantage. A simple machine is a mechanical device that changes the direction and the magnitude of a force. In general, they can be defined as the simplest mechanisms that use mechani
From playlist Mechanics

Around The Corner - How Differential Steering Works (1937)
How the automobile differential allows a vehicle to turn a corner while keeping the wheels from skidding. Differential steering From Wikipedia, the free encyclopedia https://en.wikipedia.org/wiki/Differential_steering Differential steering is the means of steering a land vehicle by apply
From playlist Robotics

Felix Klein Lecture 2022 part6
From playlist Felix Klein Lectures 2022

Laplace transforms + differential equations
Download the free PDF http://tinyurl.com/EngMathYT How to solve differential equations by the method of Laplace transforms. Such ideas are seen in university mathematics.
From playlist Engineering Mathematics YouTube Workbook
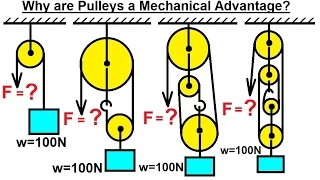
Mechanical Engineering: Particle Equilibrium (11 of 19) Why are Pulleys a Mechanical Advantage?
Visit http://ilectureonline.com for more math and science lectures! In this video I will calculate and explain the mechanical advantage of using pulleys. Next video in the Particle Equilibrium series can be seen at: http://youtu.be/XgLsBgmGigA
From playlist PHYSICS 5.5 PULLEYS AND MECHANICAL ADVANTAGE

Hélène Esnault - Motivic connections over a finite field
Correction: The affiliation of Lei Fu is Tsinghua University. Work in progress with Michael Groechenig. https://server.mcm.ac.cn/~zheng/LI/titles.html#Esnault
From playlist Conférence « Géométrie arithmétique en l’honneur de Luc Illusie » - 5 mai 2021

Resolution of singularities of complex algebraic varieties – D. Abramovich – ICM2018
Algebraic and Complex Geometry Invited Lecture 4.13 Resolution of singularities of complex algebraic varieties and their families Dan Abramovich Abstract: We discuss Hironaka’s theorem on resolution of singularities in charactetistic 0 as well as more recent progress, both on simplifying
From playlist Algebraic & Complex Geometry

Branched Holomorphic Cartan Geometries by Sorin Dumitrescu
DISCUSSION MEETING ANALYTIC AND ALGEBRAIC GEOMETRY DATE:19 March 2018 to 24 March 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore. Complex analytic geometry is a very broad area of mathematics straddling differential geometry, algebraic geometry and analysis. Much of the interactions be
From playlist Analytic and Algebraic Geometry-2018

Harmonic Maps between surfaces and Teichmuller theory (Lecture - 1) by Michael Wolf
Geometry, Groups and Dynamics (GGD) - 2017 DATE: 06 November 2017 to 24 November 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru The program focuses on geometry, dynamical systems and group actions. Topics are chosen to cover the modern aspects of these areas in which research has b
From playlist Geometry, Groups and Dynamics (GGD) - 2017

What is Special About Polynomials? (Perspectives from Coding theory and DiffGeom) - Larry Guth
What is Special About Polynomials? (Perspectives from Coding theory and Differential Geometry) Larry Guth Massachusetts Institute of Technology March 13, 2013 olynomials are a special class of functions. They are useful in many branches of mathematics, often in problems which don't mention
From playlist Mathematics

Solve the general solution for differentiable equation with trig
Learn how to solve the particular solution of differential equations. A differential equation is an equation that relates a function with its derivatives. The solution to a differential equation involves two parts: the general solution and the particular solution. The general solution give
From playlist Differential Equations
What is General Relativity? Lesson 0 and Lesson 75: Invitation and Recap
What is General Relativity? Lesson 0 and Lesson 75: Invitation and Recap This lesson is for those considering watching some or all of "What is General Relativity?" and for those who have finished some or all of the lesson. It is an invitation to the subject and also a recap of the subject
From playlist What is General Relativity?
