Polygons by the number of sides | Constructible polygons | Euclidean plane geometry
257-gon
In geometry, a 257-gon is a polygon with 257 sides. The sum of the interior angles of any non-self-intersecting 257-gon is 45,900°. (Wikipedia).

Polygons by the number of sides | Constructible polygons | Euclidean plane geometry
In geometry, a 257-gon is a polygon with 257 sides. The sum of the interior angles of any non-self-intersecting 257-gon is 45,900°. (Wikipedia).


MegaFavNumbers: The beauty of 8388608 = 2^23
A perfect sphere packing in the vector space of 23-bit numbers, which is related to the famous Golay (23,12) error correcting code. #MegaFavNumbers
From playlist MegaFavNumbers

Conversion Arcs and 2,916,485,648,612,232,232,816 (MegaFavNumbers)
I'm sorry. The MegaFavNumbers playlist: https://www.youtube.com/playlist?list=PLar4u0v66vIodqt3KSZPsYyuULD5meoAo
From playlist MegaFavNumbers

#MegaFavNumbers - 7,588,043,387,109,376 by Egi
87,109,376^2=7,588,043,387,109,376. The last 8 digits is the square root😀, it's called an automorphic number which n^2 ends with n
From playlist MegaFavNumbers

My entry in the #MegaFavNumbers project by James Grime and Matt Parker. The number in question is 2¹⁰²⁴, also known as 179,769,313,486,231,590,772,930,519,078,902,473,361,797,697,894,230,657,273,430,081,157,732,675,805,500,963,132,708,477,322,407,536,021,120,113,879,871,393,357,658,789,76
From playlist MegaFavNumbers

Heptadecagon and Fermat Primes (the math bit) - Numberphile
Main (previous) video: http://youtu.be/87uo2TPrsl8 David Eisenbud from MSRI on the math behind the 17-gon and other constructible polygons. NUMBERPHILE Website: http://www.numberphile.com/ Numberphile on Facebook: http://www.facebook.com/numberphile Numberphile tweets: https://twitter.com
From playlist David Eisenbud on Numberphile

MegaFavNumbers: All you need to go Mega is just 3 bytes
Joining the maths #MegaFavNumbers thing just because I like it. My favourity number of over 1 million is a number I remember ever since I was a child. It is used often and well known. Watch to find out why. 16777216
From playlist MegaFavNumbers

Visual Group Theory, Lecture 6.8: Impossibility proofs
Visual Group Theory, Lecture 6.8: Impossibility proofs The ancient Greeks sought basic ruler and compass constructions such as (1) squaring the circle, (2) doubling the cube, and (3) trisecting an angle. In the previous lecture, we learned how a length or angle 'z' is constructable iff th
From playlist Visual Group Theory

1,010,010,101,000,011 - #MegaFavNumbers
This is my submission to the #megafavnumbers project. My number is 1010010101000011, which is prime in bases 2, 3, 4, 5, 6 and 10. I've open-sourced my code: https://bitbucket.org/Bip901/multibase-primes Clarification: by "ignoring 1" I mean ignoring base 1, since this number cannot be fo
From playlist MegaFavNumbers

MegaFavNumbers | 8.07x10^67 vs. 137,327,459,106,673,000,000,000,000,000,000,000,000,000,000,000,000
This video compares the number of ways to shuffle a deck of cards to the number of atoms on Earth. #MegaFavNumbers 80,658,175,170,943,878,571,660,636,856,403,766,975,289,505,440,883,277,824,000,000,000,000 vs 137,327,459,106,673,000,000,000,000,000,000,000,000,000,000,000,000.00
From playlist MegaFavNumbers

Introduction to number theory lecture 14. Euler's totient function
This lecture is part of my Berkeley math 115 course "Introduction to number theory" For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj53L8sMbzIhhXSAOpuZ1Fov8 We cover the basic properties of Euler's totient function. The textbook is "An introducti
From playlist Introduction to number theory (Berkeley Math 115)
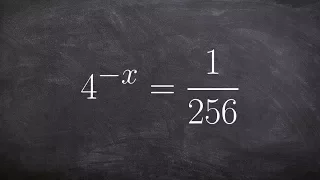
Solving an exponential equation with the base of four
👉 Learn how to solve exponential equations involving fractions. An exponential equation is an equation in which a variable occurs as an exponent. To solve an exponential equation, we make the base of both sides of the equation to be equal so that we can then equate the exponents. When the
From playlist Solve Exponential Equations with Fractions

Approximating Pi with Gregory's Theorem (visual proof for Pi day)
This is an animated visual proof of the Gregory's theorem, which provides a recursive method of finding the areas of the circumscribed 2n-gon and inscribed 2n-gon of a circle given the areas of the inscribed and circumscribed n-gons. As a Pi day treat, we show how to use these formulas to
From playlist Algebra

The Amazing Heptadecagon (17-gon) - Numberphile
More on the math behind this: http://youtu.be/oYlB5lUGlbw Catch David on the Numberphile podcast: https://youtu.be/9y1BGvnTyQA More links & stuff in full description below ↓↓↓ Professor David Eisenbud - director of MSRI - on the amazing 17-gon and its link to Gauss. See end of this video
From playlist Director's Cut on Numberphile

Happy Ending Problem - Numberphile
Professor Ron Graham discusses the famed Happy Ending Problem and Ramsey Theory. More Ron Graham Videos: http://bit.ly/Ron_Graham More links & stuff in full description below ↓↓↓ An extra little bit at: http://youtu.be/hnIBiIcuudU Graham's Number: http://youtu.be/XTeJ64KD5cg Support us o
From playlist Numberphile Videos

Ex 2: Find the Sum of an Arithmetic Series
This video explains how to find the partial sum of an arithmetic sequence given some of the terms of the series. Site: http://mathispower4u.com Blog: http://mathispower4u.wordpress.com
From playlist Series (Algebra)

This video was made for #MegaFavNumbers The sequence that is generated by cycles of bits and somehow related to prime numbers and multiplicative order of 2 mod 2n+1 Sequence: 3, 6, 15, 12, 255, 30, 63, 24, 315, 510, 33825, 60, 159783, 126, 255, 48, 65535, 630, 14942265, 1020, 4095, 67650
From playlist MegaFavNumbers
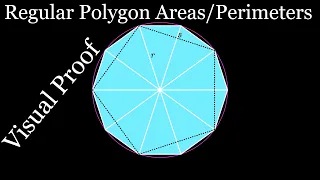
Areas and Perimeters of Regular Polygons (visual proof)
This is a short, animated visual proof demonstrating that the area of the regular 2n-gon inscribed in a circle of radius r is equal to one-half the product of r and the perimeter of the regular n-gon inscribed in the same circle. We finish with a bonus proof that the area of a circle is on
From playlist Geometry

My MegaFavNumbers - GK's Numbers with Chained Prime Factors
#MegaFavNumbers 9890836489141547229675646151234 Chained Prime Factors {2, 23, 37, 71, 101, 131, 151, 181, 191, 193, 313, 353, 373, 383, 389} visit https://oeis.org/A308101 and https://oeis.org/A308099 for details #MegaFavNumbers
From playlist MegaFavNumbers

Find the Sum of the Angles of a 16-gon
Find the Sum of the Angles of a 16-gon If you enjoyed this video please consider liking, sharing, and subscribing. Udemy Courses Via My Website: https://mathsorcerer.com My FaceBook Page: https://www.facebook.com/themathsorcerer There are several ways that you can help support my chann
From playlist Polygons