Zonal spherical function

Representation theory of Lie groups | Functional analysis | Types of functions | Harmonic analysis

In mathematics, a zonal spherical function or often just spherical function is a function on a locally compact group G with compact subgroup K (often a maximal compact subgroup) that arises as the matrix coefficient of a K-invariant vector in an irreducible representation of G. The key examples are the matrix coefficients of the spherical principal series, the irreducible representations appearing in the decomposition of the unitary representation of G on L2(G/K). In this case the commutant of G is generated by the algebra of biinvariant functions on G with respect to K acting by right convolution. It is commutative if in addition G/K is a symmetric space, for example when G is a connected semisimple Lie group with finite centre and K is a maximal compact subgroup. The matrix coefficients of the spherical principal series describe precisely the spectrum of the correspondingC* algebra generated by the biinvariant functions of compact support, often called a Hecke algebra. The spectrum of the commutative Banach *-algebra of biinvariant L1 functions is larger; when G is a semisimple Lie group with maximal compact subgroup K, additional characters come from matrix coefficients of the complementary series, obtained by analytic continuation of the spherical principal series. Zonal spherical functions have been explicitly determined for real semisimple groups by Harish-Chandra. For special linear groups, they were independently discovered by Israel Gelfand and Mark Naimark. For complex groups, the theory simplifies significantly, because G is the complexification of K, and the formulas are related to analytic continuations of the Weyl character formula on K. The abstract functional analytic theory of zonal spherical functions was first developed by Roger Godement. Apart from their group theoretic interpretation, the zonal spherical functions for a semisimple Lie group G also provide a set of simultaneous eigenfunctions for the natural action of the centre of the universal enveloping algebra of G on L2(G/K), as differential operators on the symmetric space G/K. For semisimple p-adic Lie groups, the theory of zonal spherical functions and Hecke algebras was first developed by Satake and Ian G. Macdonald. The analogues of the Plancherel theorem and Fourier inversion formula in this setting generalise the eigenfunction expansions of Mehler, Weyl and Fock for singular ordinary differential equations: they were obtained in full generality in the 1960s in terms of Harish-Chandra's c-function. The name "zonal spherical function" comes from the case when G is SO(3,R) acting on a 2-sphere and K is the subgroup fixing a point: in this case the zonal spherical functions can be regarded as certain functions on the sphere invariant under rotation about a fixed axis. (Wikipedia).

Definition of spherical coordinates | Lecture 33 | Vector Calculus for Engineers

We define the relationship between Cartesian coordinates and spherical coordinates; the position vector in spherical coordinates; the volume element in spherical coordinates; the unit vectors; and how to differentiate the spherical coordinate unit vectors. Join me on Coursera: https://www

From playlist Vector Calculus for Engineers

Introduction to Cylindrical Coordinates

This video introduces cylindrical coordinates and shows how to convert between cylindrical coordinates and rectangular coordinates. http://mathispower4u.yolasite.com/

From playlist Quadric, Surfaces, Cylindrical Coordinates and Spherical Coordinates

Introduction to Cylindrical Coordinates

Introduction to Cylindrical Coordinates Definition of a cylindrical coordinate and all of the formulas used to convert from cylindrical to rectangular and from rectangular to cylindrical. Examples are also given.

From playlist Calculus 3

Introduction to Spherical Coordinates

Introduction to Spherical Coordinates This is a full introduction to the spherical coordinate system. The definition is given and then the formulas for converting rectangular to spherical and spherical to rectangular. We also look at some of the key graphs in spherical coordinates. Final

From playlist Calculus 3

Introduction to Spherical Coordinates

This video defines spherical coordinates and explains how to convert between spherical and rectangular coordinates. http://mathispower4u.yolasite.com/

From playlist Quadric, Surfaces, Cylindrical Coordinates and Spherical Coordinates

Curved Coordinate Systems

A description of curved coordinate systems, including cylindrical and spherical coordinates, and their unit vectors.

From playlist Phys 331 Uploads

Ex 1: Convert Cartesian Coordinates to Cylindrical Coordinates

This video explains how to convert rectangular coordinates to cylindrical coordinates. Site: http://mathispower4u.com

From playlist Quadric, Surfaces, Cylindrical Coordinates and Spherical Coordinates

Converting Between Spherical and Rectangular Equations

This video provides example of how to convert between rectangular equation and spherical equations and vice versa. http://mathispower4u.com

From playlist Quadric, Surfaces, Cylindrical Coordinates and Spherical Coordinates

IITM Earth System Model: Goals, Priorities, Future Plans by R Krishnan

DISCUSSION MEETING: WORKSHOP ON CLIMATE STUDIES (HYBRID) ORGANIZERS: Rama Govindarajan (ICTS-TIFR, India), Sandeep Juneja (TIFR, India), Ramalingam Saravanan (Texas A&M University, USA) and Sandip Trivedi (TIFR, India) DATE : 01 March 2022 to 03 March 2022 VENUE: Ramanujan Lecture Hall

From playlist Workshop on Climate Studies - 2022

Positive definite kernels on spheres by E K Narayanan

DISCUSSION MEETING SPHERE PACKING ORGANIZERS: Mahesh Kakde and E.K. Narayanan DATE: 31 October 2019 to 06 November 2019 VENUE: Madhava Lecture Hall, ICTS Bangalore Sphere packing is a centuries-old problem in geometry, with many connections to other branches of mathematics (number the

From playlist Sphere Packing - 2019

11b Data Analytics: Variogram Modeling

Lecture on variogram modeling.

From playlist Data Analytics and Geostatistics

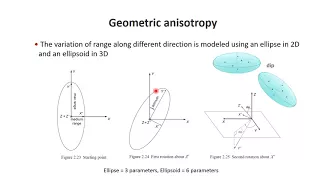
Geostatistics session 4 variogram modeling

Introduction to variogram modeling

From playlist Geostatistics GS240

11c Python Data Analytics Reboot: Variogram Modeling

Walkthrough of an interactive workflow in Python Jupyter Notebook with GeostatsPy, matplotlib and pywidgets for directional variogram calculation and modeling.

From playlist Data Analytics and Geostatistics

Jeffrey Galkowski: Geodesic beams in eigenfunction analysis (part 2 of 2)

This talk is a continuation of ‘Understanding the growth of Laplace eigenfunctions’. We explain the method of geodesic beams in detail and review the development of these techniques in the setting of defect measures. We then describe the tools and give example applications in concrete geom

From playlist Geometry

Effects of curvature, Shear flow and Non linearity on Tropical Waves by Mukesh Raghav

ICTS IN-HOUSE 2020 Organizers: Amit Kumar Chatterjee, Divya Jaganathan, Junaid Majeed, Pritha Dolai Date:: 17-18th February 2020 Venue: Ramanujan Lecture Hall, ICTS Bangalore inhouse@icts.res.in An exclusive two-day event to exchange ideas and discuss research amongst member

From playlist ICTS In-house 2020

Physics Ch 67.1 Advanced E&M: Review Vectors (88 of 113) Curl in Spherical Coordinates Ex. 1

Visit http://ilectureonline.com for more math and science lectures! To donate: http://www.ilectureonline.com/donate https://www.patreon.com/user?u=3236071 We will calculate the curl in spherical coordinates of v vector, given v=r(r-hat). Example 1 Next video in this series can be seen a

From playlist PHYSICS 67.1 ADVANCED E&M VECTORS & FIELDS

ITCZ Dynamics and Indian Monsoon: Energy Constraints (Lecture 7) by B N Goswami

ICTS Summer Course 2022 (www.icts.res.in/lectures/sc2022bng) Title : Introduction to Indian monsoon Variability, Predictability, and Teleconnections Speaker : Professor B N Goswami (Cotton University) Date : 23rd April onwards every week o

From playlist Summer Course 2022: Introduction to Indian monsoon Variability, Predictability, and Teleconnections

3D structure & maintenance of the present day observed Climate (Lecture 1) by B N Goswami

From playlist Summer Course 2022: Introduction to Indian monsoon Variability, Predictability, and Teleconnections

3D structure & maintenance of the present day observed Climate (Lecture 2) by B N Goswami

From playlist Summer Course 2022: Introduction to Indian monsoon Variability, Predictability, and Teleconnections

Cylindrical Coordinates to Rectangular Coordinates Example

Cylindrical Coordinates to Rectangular Coordinates Example If you enjoyed this video please consider liking, sharing, and subscribing. You can also help support my channel by becoming a member https://www.youtube.com/channel/UCr7lmzIk63PZnBw3bezl-Mg/join Thank you:)

From playlist Larson Calculus 11.7 Cylindrical and Spherical Coordinates

Zonal spherical function

Related pages