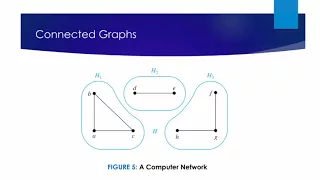
Connectedness
In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected. When a disconnected object can be split naturally into connected pieces, each piece is usually called a component (or connected component). (Wikipedia).