
Lecture 27. Properties of tensor products
0:00 Use properties of tensor products to effectively think about them! 0:50 Tensor product is symmetric 1:17 Tensor product is associative 1:42 Tensor product is additive 21:40 Corollaries 24:03 Generators in a tensor product 25:30 Tensor product of f.g. modules is itself f.g. 32:05 Tenso
From playlist Abstract Algebra 2

What is a Tensor 5: Tensor Products
What is a Tensor 5: Tensor Products Errata: At 22:00 I write down "T_00 e^0 @ e^1" and the correct expression is "T_00 e^0 @ e^0"
From playlist What is a Tensor?

A Concrete Introduction to Tensor Products
The tensor product of vector spaces (or modules over a ring) can be difficult to understand at first because it's not obvious how calculations can be done with the elements of a tensor product. In this video we give an explanation of an explicit construction of the tensor product and work
From playlist Tensor Products

Proof: Uniqueness of the Tensor Product
Universal property introduction: https://youtu.be/vZzZhdLC_YQ This video proves the uniqueness of the tensor product of vector spaces (or modules over a commutative ring). This uses the universal property of the tensor product to prove the existence of an isomorphism (linear bijection) be
From playlist Tensor Products
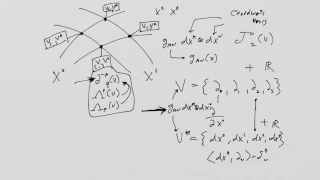
What is a Tensor? Lesson 29: Transformations of tensors and p-forms (part review)
What is a Tensor? Lesson 29: Tensor and N-form Transformations This long lesson begins with a review of tensor product spaces and the relationship between coordinate transformations on spacetime and basis transformations of tensor fields. Then we do a full example to introduce the idea th
From playlist What is a Tensor?

What is a Tensor 6: Tensor Product Spaces
What is a Tensor 6: Tensor Product Spaces There is an error at 15:00 which is annotated but annotations can not be seen on mobile devices. It is a somewhat obvious error! Can you spot it? :)
From playlist What is a Tensor?

What Is A Tensor Lesson #1: Elementary vector spaces
We define a vector space and lay the foundation of a solid understanding of tensors.
From playlist What is a Tensor?

Commutative algebra 20 Tensor products review
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. In this lecture we review the definition of the tensor product of R-modules. We calculate the tensor products in the cases of
From playlist Commutative algebra

Calculus 3: Tensors (1 of 28) What is a Tensor?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is a tensor. A tensor is a mathematical representation of a scalar (tensor of rank 0), a vector (tensor of rank 1), a dyad (tensor of rank 2), a triad (tensor or rank 3). Next video in t
From playlist CALCULUS 3 CH 10 TENSORS
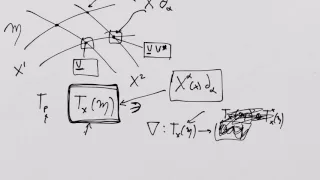
What is a Tensor? Lesson 16: The metric tensor field
What is a Tensor? Lesson 16: The metric tensor field
From playlist What is a Tensor?

What is a Tensor? Lesson 20: Algebraic Structures II - Modules to Algebras
What is a Tensor? Lesson 20: Algebraic Structures II - Modules to Algebras We complete our survey of the basic algebraic structures that appear in the study of general relativity. Also, we develop the important example of the tensor algebra.
From playlist What is a Tensor?
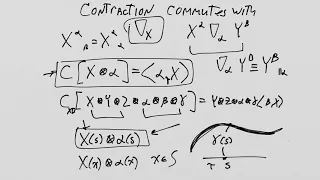
What is General Relativity? Lesson 14: The covariant derivative of a covector
We start by demonstrating that contraction commutes with directional covariant derivative and then derive the CFREE and COMP expressions for the covariant derivative of a covector.
From playlist What is General Relativity?

What is General Relativity? Lesson 13 Some important CFREE relations
We prove some critical CFREE expressions required for the derivation of the metric connection. Errata: At 46:00 the argument should have the vector "Z" not the vector "X". X is part of the example tensor and Z is being fed to the tensor.
From playlist What is General Relativity?

Rings 11 Tensor products of modules
This lecture is part of an online course on rings and modules. We define tensor prducts of modules over more general rings, and give some examples: coproducts of commutative rings, tensors in differential geometry, tensor products of group representations, and tensor products of fields.
From playlist Rings and modules

Lecture 7 | Quantum Entanglements, Part 3 (Stanford)
Lecture 7 of Leonard Susskind's course concentrating on Quantum Entanglements (Part 3, Spring 2007). Recorded May 21, 2007 at Stanford University. This Stanford Continuing Studies course is the third of a three-quarter sequence of classes exploring the "quantum entanglements" in modern
From playlist Lecture Collection | Quantum Entanglements: Part 3 (Spring 2007)
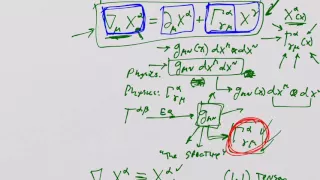
What is a Tensor? Lesson 18: The covariant derivative continued
What is a Tensor? Lesson 18: The covariant derivative continued This lesson covers some of the "coordinate free" language used to describe the covariant derivative. As a whole this lecture is optional. However, becoming comfortable with coordinate free language is probably a good idea. I
From playlist What is a Tensor?

What is General Relativity? Lesson 15 The covariant derivative of a (p,q)-rank tensor
In this lesson we review all the CFREE algebraic rules and the COMP conversions and then demonstrate the CFREE and COMP formulas for the covariant derivative of an arbitrary tensor.
From playlist What is General Relativity?

Log Volume Computations - part 0.2 - Total Rings Of Fractions
This is the second part of the prerequisite videos for the log volume computations and is optional for continuing. In this video we explain how to take rings of fractions for reduced but not irreducible rings. We then show that the ring of fractions of a tensor product is the tensor prod
From playlist Log Volume Computations

Rings 10 Tensor products of abelian groups
This lecture is part of an online course on rings and modules. We define tensor products of abelian groups, and calculate them for many common examples using the fact that tensor products preserve colimits. For the other lectures in the course see https://www.youtube.com/playlist?list=P
From playlist Rings and modules

On the classification of fusion categories – Sonia Natale – ICM2018
Algebra Invited Lecture 2.5 On the classification of fusion categories Sonia Natale Abstract: We report, from an algebraic point of view, on some methods and results on the classification problem of fusion categories over an algebraically closed field of characteristic zero. © Interna
From playlist Algebra