
Field Theory - Splitting Fields in CC - Lecture 11
In this video we compute some examples of splitting fields over CC. These include a Kummer field, a cyclotomic field, a quadratic field, and some real cubic field.
From playlist Field Theory

Galois theory: Splitting fields
This lecture is part of an online course on Galois theory. We define the splitting field of a polynomial p over a field K (a field that is generated by roots of p and such that p splits into linear factors). We give a few examples, and show that it exists and is unique up to isomorphism
From playlist Galois theory

Physics - E&M: Ch 36.1 The Electric Field Understood (1 of 17) What is an Electric Field?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is an electric field. An electric field exerts a force on a charged place in the field, can be detected by placing a charged in the field and observing the effect on the charge. The stren
From playlist THE "WHAT IS" PLAYLIST

FIT3.1.3. Example of Splitting Field
Field Theory: Let f(x) = x^4 -16x^2 +4. We find the roots of f(x), calculate the splitting field K of f(x) over Q in C, and determine the automorphism group of K.
From playlist Abstract Algebra

Physics 36 The Electric Field (5 of 18) The Electric Dipole
Visit http://ilectureonline.com for more math and science lectures! In this video I will find the electric field of the electric dipole.
From playlist PHYSICS 22 E&M THE ELECTRIC FIELD

From playlist E Field Lectures
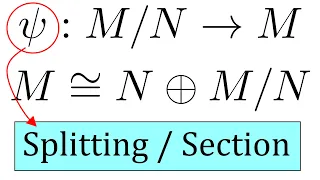
Splitting Homomorphism of R-Modules
A splitting, or section, is a homomorphism from the quotient module to the original module that gives a representative for each coset. If we have a splitting, we can prove that the module is isomorphic to a direct sum! This video is an explanation of how the splitting leads to an isomorphi
From playlist Ring & Module Theory
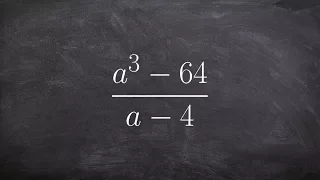
How to synthetic divide when you are missing values
👉 Learn about dividing by synthetic division when there is a missing power. Synthetic division is a method of dividing polynomials by linear expressions. To divide using synthetic division, we equate the divisor to 0 and then solve for the variable, the solution for the variable will be th
From playlist Divide Polynomials using Synthetic Division

Worldwide Calculus: Conservative Vector Fields
Lecture on 'Conservative Vector Fields' from 'Worldwide Multivariable Calculus'. For more lecture videos and $10 digital textbooks, visit www.centerofmath.org.
From playlist Integration and Vector Fields
28. Transition Metals: Crystal Field Theory Part I
MIT 5.111 Principles of Chemical Science, Fall 2014 View the complete course: https://ocw.mit.edu/5-111F14 Instructor: Catherine Drennan Crystal field theory was developed to explain the special features of transition metal complexes, including their beautiful colors and their magnetic pr
From playlist MIT 5.111 Principles of Chemical Science, Fall 2014

Lec 28 | MIT 5.111 Principles of Chemical Science, Fall 2005
Transition Metals: Crystal Field Theory (Prof. Catherine Drennan) View the complete course: http://ocw.mit.edu/5-111F05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 5.111 Principles of Chemical Science, Fall 2005
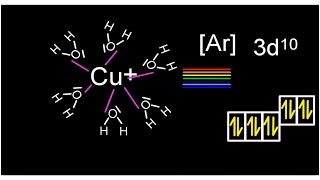
Periodicity and crystal field theory
IB Chemistry Lesson on why coloured transition metal complexes form.
From playlist IB Chemistry

On a Hecke algebra isomorphism of Kazhdan by Radhika Ganapathy
PROGRAM GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fund
From playlist Group Algebras, Representations And Computation

Lec 30 | MIT 5.111 Principles of Chemical Science, Fall 2005
Transition Metals (Prof. Catherine Drennan) View the complete course: http://ocw.mit.edu/5-111F05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 5.111 Principles of Chemical Science, Fall 2005

Visual Group Theory, Lecture 6.5: Galois group actions and normal field extensions
Visual Group Theory, Lecture 6.5: Galois group actions and normal field extensions If f(x) has a root in an extension field F of Q, then any automorphism of F permutes the roots of f(x). This means that there is a group action of Gal(f(x)) on the roots of f(x), and this action has only on
From playlist Visual Group Theory
Gopal Prasad: Descent in Bruhat-Tits theory
Bruhat-Tits theory applies to a semisimple group G, defined over an henselian discretly valued field K, such that G admits a Borel K-subgroup after an extension of K. The construction of the theory goes then by a deep Galois descent argument for the building and also for the parahoric grou
From playlist Algebraic and Complex Geometry
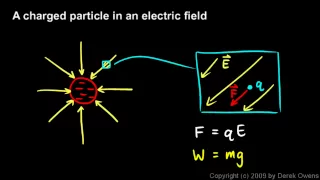
Physics 12.3.2b - A Charged Particle in an Electric Field
A description of the force on a charged particle in an electric field. F = qE. From the physics course by Derek Owens. The distance learning course is available at http://www.derekowens.com
From playlist Physics - Electric Fields
