
Is it a monomial, binomial, trinomial, or polynomial
👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different interger exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials

Is it a polynomial with two variables
👉 Learn how to determine whether a given equation is a polynomial or not. A polynomial function or equation is the sum of one or more terms where each term is either a number, or a number times the independent variable raised to a positive integer exponent. A polynomial equation of functio
From playlist Is it a polynomial or not?

Summary for classifying polynomials
👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different interger exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials

👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different interger exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials

Galois theory: Separable extensions
This lecture is part of an online graduate course on Galois theory. We define separable algebraic extensions, and give some examples of separable and non-separable extensions. At the end we briefly discuss purely inseparable extensions.
From playlist Galois theory

FIT3.1.1. Roots of Polynomials
Field Theory: We recall basic factoring results for polynomials from Ring Theory and give a definition of a splitting field. This allows one to consider any irreducible polynomial as a set of roots, and in turn we consider when an irreducible polynomial can have multiple roots. We finish
From playlist Abstract Algebra

Calculus 1 Lecture 1.2 Part 2: Properties of Limits. Techniques of Limit Computation
From playlist Calculus 1 Playlist 1
Daniel Bertrand: Generalized Jacobians and Pellian polynomials
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Number Theory

How to determine if a term is a monomial or not
👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different interger exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials

Learn how to write a polynomial in standard form and classify
👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different integer exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials | Equations

Haotian Jiang: Minimizing Convex Functions with Integral Minimizers
Given a separation oracle SO for a convex function f that has an integral minimizer inside a box with radius R, we show how to find an exact minimizer of f using at most • O(n(n + log(R))) calls to SO and poly(n,log(R)) arithmetic operations, or • O(nlog(nR)) calls to SO and exp(O(n)) · po
From playlist Workshop: Continuous approaches to discrete optimization

Thieu Vo, Ton Duc Thang University
April 2, Thieu Vo, Ton Duc Thang University Rational solutions of first-order algebraic difference equations
From playlist Spring 2021 Online Kolchin Seminar in Differential Algebra

Monotone Arithmetic Circuit Lower Bounds Via Communication Complexity - Arkadev Chattopadhyay
Computer Science/Discrete Mathematics Seminar I Topic: Monotone Arithmetic Circuit Lower Bounds Via Communication Complexity Speaker: Arkadev Chattopadhyay Affiliation: Tata Institute of Fundamental Research Date: February 15, 2021 For more video please visit http://video.ias.edu
From playlist Mathematics

Sarah Post: Rational extensions of superintegrable systems, exceptional polynomials & Painleve eq.s
Abstract: In this talk, I will discuss recent work with Ian Marquette and Lisa Ritter on superintegable extensions of a Smorodinsky Winternitz potential associated with exception orthogonal polynomials (EOPs). EOPs are families of orthogonal polynomials that generalize the classical ones b
From playlist Integrable Systems 9th Workshop

Introduction to Spherical Harmonics
Using separation of variables in spherical coordinates, we arrive at spherical harmonics.
From playlist Quantum Mechanics Uploads

Classify a polynomial and determine degree and leading coefficient
👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different integer exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials | Equations
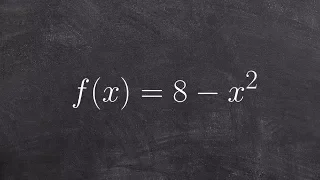
Classify a polynomial and determine degree and leading coefficient
👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different integer exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials | Equations

Classify a polynomial and determine degree and leading coefficient
👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different integer exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials | Equations

Nijenhuis geometry for ECRs: Pre-recorded Lecture 2 Part A
Pre-recorded Lecture 2 Part A: Nijenhuis geometry for ECRs Date: 9 February 2022 Lecture slides: https://mathematical-research-institute.sydney.edu.au/wp-content/uploads/2022/02/Prerecorded_Lecture2.pdf ---------------------------------------------------------------------------------------
From playlist MATRIX-SMRI Symposium: Nijenhuis Geometry and integrable systems

Classify a polynomial and determine degree and leading coefficient
👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different integer exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials | Equations