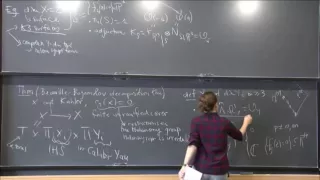Symplectic geometry
Symplectic geometry is a branch of differential geometry and differential topology that studies symplectic manifolds; that is, differentiable manifolds equipped with a closed, nondegenerate 2-form. Symplectic geometry has its origins in the Hamiltonian formulation of classical mechanics where the phase space of certain classical systems takes on the structure of a symplectic manifold. The term "symplectic", introduced by Weyl, is a calque of "complex"; previously, the "symplectic group" had been called the "line complex group". "Complex" comes from the Latin com-plexus, meaning "braided together" (co- + plexus), while symplectic comes from the corresponding Greek sym-plektikos (συμπλεκτικός); in both cases the stem comes from the Indo-European root *pleḱ- The name reflects the deep connections between complex and symplectic structures. By Darboux's Theorem, symplectic manifolds are isomorphic to the standard symplectic vector space locally, hence only have global (topological) invariants. "Symplectic topology," which studies global properties of symplectic manifolds, is often used interchangeably with "symplectic geometry." The name "complex group" formerly advocated by me in allusion to line complexes, as these are defined by the vanishing of antisymmetric bilinear forms, has become more and more embarrassing through collision with the word "complex" in the connotation of complex number. I therefore propose to replace it by the corresponding Greek adjective "symplectic." Dickson called the group the "Abelian linear group" in homage to Abel who first studied it. , p. 165) (Wikipedia).
