
The TRUTH about TENSORS, Part 9: Vector Bundles
In this video we define vector bundles in full abstraction, of which tangent bundles are a special case.
From playlist The TRUTH about TENSORS

The TRUTH about TENSORS, Part 10: Frames
What do the octonions have to do with spheres? Skip to the end of the video to find out!
From playlist The TRUTH about TENSORS

What Is A Tensor Lesson #1: Elementary vector spaces
We define a vector space and lay the foundation of a solid understanding of tensors.
From playlist What is a Tensor?

What is a Tensor? Lesson 11: The metric tensor
What is a Tensor 11: The Metric Tensor
From playlist What is a Tensor?

Introduction to Fiber Bundles part 1: Definitions
We give the definition of a fiber bundle with fiber F, trivializations and transition maps. This is a really basic stuff that we use a lot. Here are the topics this sets up: *Associated Bundles/Principal Bundles *Reductions of Structure Groups *Steenrod's Theorem *Torsor structure on arith
From playlist Fiber bundles

The TRUTH about TENSORS, Part 8: Tangent bundles & vector fields
In this video, we discuss the definition of the tangent bundle of a manifold, which in turns inspires the more general definition of vector bundles, to be discussed in the next video. The notion of tangent bundle, further lets us formalize our intuitive notion of vector fields.
From playlist The TRUTH about TENSORS

Jose Perea (6/15/22): Vector bundles for data alignment and dimensionality reduction
A vector bundle can be thought of as a family of vector spaces parametrized by a fixed topological space. Vector bundles have rich structure, and arise naturally when trying to solve synchronization problems in data science. I will show in this talk how the classical machinery (e.g., class
From playlist AATRN 2022
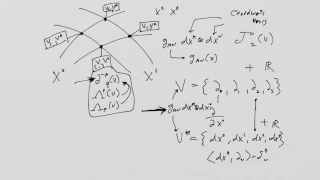
What is a Tensor? Lesson 29: Transformations of tensors and p-forms (part review)
What is a Tensor? Lesson 29: Tensor and N-form Transformations This long lesson begins with a review of tensor product spaces and the relationship between coordinate transformations on spacetime and basis transformations of tensor fields. Then we do a full example to introduce the idea th
From playlist What is a Tensor?

Perfectoid spaces (Lecture 5) by Kiran Kedlaya
PERFECTOID SPACES ORGANIZERS: Debargha Banerjee, Denis Benois, Chitrabhanu Chaudhuri, and Narasimha Kumar Cheraku DATE & TIME: 09 September 2019 to 20 September 2019 VENUE: Madhava Lecture Hall, ICTS, Bangalore Scientific committee: Jacques Tilouine (University of Paris, France) Eknath
From playlist Perfectoid Spaces 2019
What is a Vector Space? (Abstract Algebra)
Vector spaces are one of the fundamental objects you study in abstract algebra. They are a significant generalization of the 2- and 3-dimensional vectors you study in science. In this lesson we talk about the definition of a vector space and give a few surprising examples. Be sure to su
From playlist Abstract Algebra

Daxin Xu - Parallel transport for Higgs bundles over p-adic curves
Faltings conjectured that under the p-adic Simpson correspondence, finite dimensional p-adic representations of the geometric étale fundamental group of a smooth proper p-adic curve X are equivalent to semi-stable Higgs bundles of degree zero over X. We will talk about an equivalence betwe
From playlist Franco-Asian Summer School on Arithmetic Geometry (CIRM)

Kac polynomials and Lie algebras associated to quivers and curves – Olivier Schiffmann – ICM2018
Lie Theory and Generalizations Invited Lecture 7.1 Kac polynomials and Lie algebras associated to quivers and curves Olivier Schiffmann Abstract: We provide an explicit formula for the following enumerative problem: how many (absolutely) indecomposable vector bundles of a given rank r an
From playlist Lie Theory and Generalizations

A. Höring - A decomposition theorem for singular spaces with trivial canonical class (Part 3)
The Beauville-Bogomolov decomposition theorem asserts that any compact Kähler manifold with numerically trivial canonical bundle admits an étale cover that decomposes into a product of a torus, an irreducible, simply-connected Calabi-Yau, and holomorphic symplectic manifolds. With the deve
From playlist Ecole d'été 2019 - Foliations and algebraic geometry

An introduction to spectral data for Higgs bundles.. by Laura Schaposnik
Higgs bundles URL: http://www.icts.res.in/program/hb2016 DATES: Monday 21 Mar, 2016 - Friday 01 Apr, 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore DESCRIPTION: Higgs bundles arise as solutions to noncompact analog of the Yang-Mills equation. Hitchin showed that irreducible solutio
From playlist Higgs Bundles

H. Guenancia - A decomposition theorem for singular spaces with trivial canonical class (Part 1)
The Beauville-Bogomolov decomposition theorem asserts that any compact Kähler manifold with numerically trivial canonical bundle admits an étale cover that decomposes into a product of a torus, an irreducible, simply-connected Calabi-Yau, and holomorphic symplectic manifolds. With the deve
From playlist Ecole d'été 2019 - Foliations and algebraic geometry

Fargues' conjecture in the GL_2-case by Ildar Gaisin
PERFECTOID SPACES ORGANIZERS: Debargha Banerjee, Denis Benois, Chitrabhanu Chaudhuri, and Narasimha Kumar Cheraku DATE & TIME: 09 September 2019 to 20 September 2019 VENUE: Madhava Lecture Hall, ICTS, Bangalore Scientific committee: Jacques Tilouine (University of Paris, France) Eknath
From playlist Perfectoid Spaces 2019

Geometry of vortices on Riemann surfaces (Lecture 2) by Oscar García-Prada
PROGRAM: VORTEX MODULI ORGANIZERS: Nuno Romão (University of Augsburg, Germany) and Sushmita Venugopalan (IMSc, India) DATE & TIME: 06 February 2023 to 17 February 2023 VENUE: Ramanujan Lecture Hall, ICTS Bengaluru For a long time, the vortex equations and their associated self-dual fie
From playlist Vortex Moduli - 2023

Multivariable Calculus | The notion of a vector and its length.
We define the notion of a vector as it relates to multivariable calculus and define its length. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Vectors for Multivariable Calculus

Automorphism group of the moduli space of parabolic vector bundles by David Alfaya Sanchez
DISCUSSION MEETING ANALYTIC AND ALGEBRAIC GEOMETRY DATE:19 March 2018 to 24 March 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore. Complex analytic geometry is a very broad area of mathematics straddling differential geometry, algebraic geometry and analysis. Much of the interactions be
From playlist Analytic and Algebraic Geometry-2018
