
The TRUTH about TENSORS, Part 9: Vector Bundles
In this video we define vector bundles in full abstraction, of which tangent bundles are a special case.
From playlist The TRUTH about TENSORS

This video explains the definition of a vector space and provides examples of vector spaces.
From playlist Vector Spaces

The TRUTH about TENSORS, Part 10: Frames
What do the octonions have to do with spheres? Skip to the end of the video to find out!
From playlist The TRUTH about TENSORS

Algebra 1M - international Course no. 104016 Dr. Aviv Censor Technion - International school of engineering
From playlist Algebra 1M

The TRUTH about TENSORS, Part 8: Tangent bundles & vector fields
In this video, we discuss the definition of the tangent bundle of a manifold, which in turns inspires the more general definition of vector bundles, to be discussed in the next video. The notion of tangent bundle, further lets us formalize our intuitive notion of vector fields.
From playlist The TRUTH about TENSORS

Vector Calculus 1: What Is a Vector?
https://bit.ly/PavelPatreon https://lem.ma/LA - Linear Algebra on Lemma http://bit.ly/ITCYTNew - Dr. Grinfeld's Tensor Calculus textbook https://lem.ma/prep - Complete SAT Math Prep
From playlist Vector Calculus

What is a Tensor? Lesson 11: The metric tensor
What is a Tensor 11: The Metric Tensor
From playlist What is a Tensor?

Branched Holomorphic Cartan Geometries by Sorin Dumitrescu
DISCUSSION MEETING ANALYTIC AND ALGEBRAIC GEOMETRY DATE:19 March 2018 to 24 March 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore. Complex analytic geometry is a very broad area of mathematics straddling differential geometry, algebraic geometry and analysis. Much of the interactions be
From playlist Analytic and Algebraic Geometry-2018

Hilbert Space Techniques in Complex Analysis and Geometry (Lecture 1) by Dror Varolin
PROGRAM CAUCHY-RIEMANN EQUATIONS IN HIGHER DIMENSIONS ORGANIZERS: Sivaguru, Diganta Borah and Debraj Chakrabarti DATE: 15 July 2019 to 02 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Complex analysis is one of the central areas of modern mathematics, and deals with holomo
From playlist Cauchy-Riemann Equations in Higher Dimensions 2019
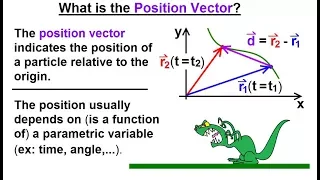
Calculus 3: Vector Calculus in 2D (17 of 39) What is the Position Vector?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is the position vector. The position vector indicates the position of a particle relative to the origin. The position usually depends on, or is a function of, a parametric variable (ex. t
From playlist CALCULUS 3 CH 3 VECTOR CALCULUS

Jacob Lurie: A Riemann-Hilbert Correspondence in p-adic Geometry Part 1
At the start of the 20th century, David Hilbert asked which representations can arise by studying the monodromy of Fuchsian equations. This question was the starting point for a beautiful circle of ideas relating the topology of a complex algebraic variety X to the study of algebraic diffe
From playlist Felix Klein Lectures 2022

Holomorphic Cartan geometries on simply connected manifolds by Sorin Dumitrescu
Discussion Meeting Complex Algebraic Geometry ORGANIZERS: Indranil Biswas, Mahan Mj and A. J. Parameswaran DATE:01 October 2018 to 06 October 2018 VENUE: Madhava Lecture Hall, ICTS, Bangalore The discussion meeting on Complex Algebraic Geometry will be centered around the "Infosys-ICT
From playlist Complex Algebraic Geometry 2018

Holomorphic rigid geometric structures on compact manifolds by Sorin Dumitrescu
Higgs bundles URL: http://www.icts.res.in/program/hb2016 DATES: Monday 21 Mar, 2016 - Friday 01 Apr, 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore DESCRIPTION: Higgs bundles arise as solutions to noncompact analog of the Yang-Mills equation. Hitchin showed that irreducible solutio
From playlist Higgs Bundles

Zhaoting Wei: Determinant line bundles and cohesive modules
Talk by Zhaoting Wei in Global Noncommutative Geometry Seminar (Americas) https://www.math.wustl.edu/~xtang/NCG-Seminar on December 16, 2020
From playlist Global Noncommutative Geometry Seminar (Americas)

Dror Varolin - Minicourse - Lecture 1
Dror Varolin Variations of Holomorphic Hilbert spaces Traditional complex analysis focuses on a single space, like a domain in Euclidean space, or more generally a complex manifold, and studies holomorphic maps on that space, into some target space. The typical target space for a domain i
From playlist Maryland Analysis and Geometry Atelier

Mini course 2: Introduction to Higgs bundles (Lecture 2) by Francois Labourie
Geometry, Groups and Dynamics (GGD) - 2017 DATE: 06 November 2017 to 24 November 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru The program focuses on geometry, dynamical systems and group actions. Topics are chosen to cover the modern aspects of these areas in which research has b
From playlist Geometry, Groups and Dynamics (GGD) - 2017

Kyle Broder -- Recent Developments Concerning the Schwarz Lemma
A lecture I gave at the Beijing International Center for Mathematical Research geometric analysis seminar. The title being Recent Developments Concerning the Schwarz Lemma with applications to the Wu--Yau Theorem. This contains some recent results concerning the Bochner technique for the G
From playlist Research Lectures

Multivariable Calculus | The notion of a vector and its length.
We define the notion of a vector as it relates to multivariable calculus and define its length. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Vectors for Multivariable Calculus

Coherent sheaves, Chern character, and RRG
Distinguished Lecture Series by Jean-Michel Bismut (Université Paris-Saclay, France)
From playlist Distinguished Visitors Lecture Series
