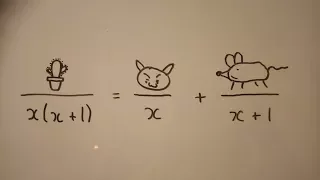
Partialbruchzerlegung: Eine Einführung
Heute behandeln wir die Partialbruchzerlegung. Hierbei handelt es sich nur um eine kleine Einführung um die Verfahrensweise zu verstehen. An introduction to partial fraction decomposition - German version
From playlist Theorie und Beweise

This video defines what a simplified fraction is and explains how to simplify fractions using prime factors and division.
From playlist Simplifying Fractions

Ever wondered what a partial sum is? The simple answer is that a partial sum is actually just the sum of part of a sequence. You can find a partial sum for both finite sequences and infinite sequences. When we talk about the sum of a finite sequence in general, we’re talking about the sum
From playlist Popular Questions

Partial Sums (1 of 2: Adding up terms in an arithmetic progression)
More resources available at www.misterwootube.com
From playlist Modelling Financial Situations

Partial fractions are SPECIAL! (Repeated linear factors)
► My Integrals course: https://www.kristakingmath.com/integrals-course The tricky thing about partial fractions is that there are four kinds of partial fractions problems. The kind of partial fractions decomposition you'll need to perform depends on the kinds of factors in your denominato
From playlist Integrals

Partial fractions + integration
Free ebook http://tinyurl.com/EngMathYT An example on how to integrate using partial fractions.
From playlist A second course in university calculus.

Fraction Forms and Open Problems
More resources available at www.misterwootube.com
From playlist Fractions, Decimals and Percentages

Representation theory and geometry – Geordie Williamson – ICM2018
Plenary Lecture 17 Representation theory and geometry Geordie Williamson Abstract: One of the most fundamental questions in representation theory asks for a description of the simple representations. I will give an introduction to this problem with an emphasis on the representation theor
From playlist Plenary Lectures

Hypersurface Singularities and Spectral Invariants - Yusuke Kawamoto
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Zoominar Topic: Hypersurface Singularities and Spectral Invariants Speaker: Yusuke Kawamoto Affiliation: ETH Zurich Date: February 17, 2023 We discuss the relation between hypersurface singularities (e.g. ADE, E˜6,E˜7,E˜8,
From playlist Mathematics

Integration & partial fractions
Free ebook http://tinyurl.com/EngMathYT An example of how to integrate using partial fractions (with repeated factors).
From playlist A second course in university calculus.

Free ebook http://tinyurl.com/EngMathYT An example on how to integrate quickly using partial fractions.
From playlist A second course in university calculus.

A p-adic monodromy theorem for de Rham local systems - Koji Shimizu
Joint IAS/Princeton University Number Theory Seminar Topic: A p-adic monodromy theorem for de Rham local systems Speaker: Koji Shimizu Affiliation: Member, School of Mathematics Date: February 27, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Alessandro Giacchetto - The Negative Side of Witten’s Conjecture
In 2017, Norbury introduced a collection of cohomology classes on the moduli space of curves, and predicted that their intersection with psi classes solves the KdV hierarchy. In a joint work in progress with N. Chidambaram and E. Garcia-Failde, we consider a deformation of Norbury’s class
From playlist Workshop on Quantum Geometry

Decomposition theorem for semisimple algebraic holonomic D-modules - Takuro Mochizuki
Members' Seminar Topic: Decomposition theorem for semisimple algebraic holonomic D-modules Speaker: Takuro Mochizuki Affiliation: Kyoto University Date: November 13, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Jean-François Dat - 2/2 On Moduli Spaces of Local Langlands Parameters
The moduli space of local Langlands parameters plays a key role in the formulation of some recent enhancements of the original local Langlands correspondence, such as the "local Langlands correspondence in families" and various "categorifications/geometrizations of LLC". We will explain
From playlist 2022 Summer School on the Langlands program

A Controlled Mather Thurston Theorem - Mike Freedman
Workshop on the h-principle and beyond Topic: A Controlled Mather Thurston Theorem Speaker: Mike Freedman Affiliation: Microsoft Date: November 03, 2021 Abstract: The "c-principle" is a cousin of Gromov's h-principle in which cobordism rather than homotopy is required to (canonically) s
From playlist Mathematics

Quiver moduli and applications, Markus Reineke (Bochum), Lecture 3
Quiver moduli spaces are algebraic varieties encoding the continuous parameters of linear algebra type classification problems. In recent years their topological and geometric properties have been explored, and applications to, among others, Donaldson-Thomas and Gromov-Witten theory have
From playlist Felix Klein Lectures 2020: Quiver moduli and applications, Markus Reineke (Bochum)
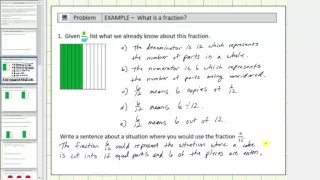
Describing the Meaning of a Fraction
This video reviews the meaning of a fraction and introduces the meaning of a simplified fraction.
From playlist Introduction to Fractions

