Direct sum

Abstract algebra

The direct sum is an operation between structures in abstract algebra, a branch of mathematics. It is defined differently, but analogously, for different kinds of structures. To see how the direct sum is used in abstract algebra, consider a more elementary kind of structure, the abelian group. The direct sum of two abelian groups and is another abelian group consisting of the ordered pairs where and . To add ordered pairs, we define the sum to be ; in other words addition is defined coordinate-wise. For example, the direct sum , where is real coordinate space, is the Cartesian plane, . A similar process can be used to form the direct sum of two vector spaces or two modules. We can also form direct sums with any finite number of summands, for example , provided and are the same kinds of algebraic structures (e.g., all abelian groups, or all vector spaces). This relies on the fact that the direct sum is associative up to isomorphism. That is, for any algebraic structures , , and of the same kind. The direct sum is also commutative up to isomorphism, i.e. for any algebraic structures and of the same kind. The direct sum of finitely many abelian groups, vector spaces, or modules is canonically isomorphic to the corresponding direct product. This is false, however, for some algebraic objects, like nonabelian groups. In the case where infinitely many objects are combined, the direct sum and direct product are not isomorphic, even for abelian groups, vector spaces, or modules. As an example, consider the direct sum and direct product of (countably) infinitely many copies of the integers. An element in the direct product is an infinite sequence, such as (1,2,3,...) but in the direct sum, there is a requirement that all but finitely many coordinates be zero, so the sequence (1,2,3,...) would be an element of the direct product but not of the direct sum, while (1,2,0,0,0,...) would be an element of both. Often, if a + sign is used, all but finitely many coordinates must be zero, while if some form of multiplication is used, all but finitely many coordinates must be 1. In more technical language, if the summands are , the direct sum is defined to be the set of tuples with such that for all but finitely many i. The direct sum is contained in the direct product , but is strictly smaller when the index set is infinite, because an element of the direct product can have infinitely many nonzero coordinates. (Wikipedia).

Direct Sum

Direct Sum definition In this video, I define the notion of direct sum of n subspaces and show what it has to do with eigenvectors. Direct sum of two subspaces: https://youtu.be/GjbMddz0Qxs Check out my Diagonalization playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmCSovHY6c

From playlist Diagonalization

Direct Sum

Have you ever wondered how to sum two mathematical objects in an elegant way? Then this video is for you! In this video, I define the sum of two vector spaces and show something neat: If you add two bases together, you get a basis for the direct sum! Finally, I generalize this notion to di

From playlist Vector Spaces

What are partial sums?

Ever wondered what a partial sum is? The simple answer is that a partial sum is actually just the sum of part of a sequence. You can find a partial sum for both finite sequences and infinite sequences. When we talk about the sum of a finite sequence in general, we’re talking about the sum

From playlist Popular Questions

Direct proportion 3

From playlist Proportion

25 - Direct sums of subspaces

Algebra 1M - international Course no. 104016 Dr. Aviv Censor Technion - International school of engineering

From playlist Algebra 1M

Determining the sum of a geometric sum when there is no sum

👉 Learn how to find the geometric sum of a series. A series is the sum of the terms of a sequence. A geometric series is the sum of the terms of a geometric sequence. The formula for the sum of n terms of a geometric sequence is given by Sn = a[(r^n - 1)/(r - 1)], where a is the first term

From playlist Series

What is the sum of an arithmetic series using the sum formula

👉 Learn how to find the partial sum of an arithmetic series. A series is the sum of the terms of a sequence. An arithmetic series is the sum of the terms of an arithmetic sequence. The formula for the sum of n terms of an arithmetic sequence is given by Sn = n/2 [2a + (n - 1)d], where a is

From playlist Series

Direct Proportion Explained & Examples - GCSE Maths Help

Direct proportion explained step by step, including proportion graphs and direct proportion GCSE maths exam style questions! Algebraic proportion is for higher GCSE maths students only. DOWNLOAD THE QUESTIONS HERE: https://drive.google.com/file/d/1UQxnek_9NOfFLgI4fPqRRXt2-ub0treK/view?us

From playlist Direct & Inverse Proportion Explained - GCSE Maths minis

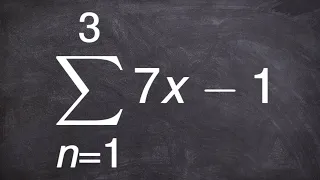
Finding the sum or an arithmetic series using summation notation

From playlist Series

Lesson 4 Module 2

From playlist Eureka Math Grade 7 Module 2

Lecture 1 | Random polytopes | Zakhar Kabluchko | EIMI

Online school "Randomness online" November 4 – 8, 2020 https://indico.eimi.ru/event/40/

From playlist Talks of Mathematics Münster's reseachers

Proof: Structure Theorem for Finitely Generated Torsion Modules Over a PID

This video has chapters to make the proof easier to follow. Splitting explanation: https://youtu.be/ZINtBNje_08 In this video we give a proof of the classification theorem using two smaller proofs by induction. We show both the elementary divisor form and the invariant factor form of a m

From playlist Ring & Module Theory

An incline, 2 masses, and a pulley. What could be more fun?

A 55 g mass is attached to a light string, which is placed over a frictionless, massless pulley, and attached to a 199 g block which is on a board inclined at 39.3° as shown. Assuming the block starts at rest and the μk between the incline and block is 0.38, how long will it take the block

From playlist JEE Physics Unit 3 - Laws of Motion and NEET Unit III - Laws of Motion

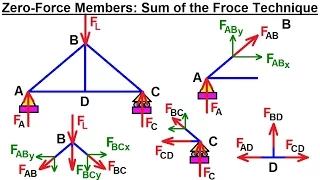
Mechanical Engineering: Trusses, Bridges & Other Structures (23 of 34) Sum of Forces Technique

Visit http://ilectureonline.com for more math and science lectures! In this video I will explain the rules of finding the zero-force members using the sum of the forces technique. Next video in this series can be seen at: https://youtu.be/as8SUXyDhNE

From playlist MECHANICAL ENGINEERING 8 TRUSSES AND BRIDGES

[Lesson 20] QED Prerequisites: Field Potentials from the Principle of Least Action

This is a repost of Lesson 20 regarding the development of the electromagnetic field potential. The first post was low video quality and had some annoying errors! In this lesson we use insight from the Lorentz force law to guide us to finding an expression for the electromagnetic field po

From playlist QED- Prerequisite Topics

Direct Products of Groups (Abstract Algebra)

The direct product is a way to combine two groups into a new, larger group. Just as you can factor integers into prime numbers, you can break apart some groups into a direct product of simpler groups. Be sure to subscribe so you don't miss new lessons from Socratica: http://bit.ly/1ixuu

From playlist Abstract Algebra

The Math You Didn't Learn | #SoME2

Sometimes people wonder what actual mathematicians do. Do they crunch large numbers? Participate in competitions with each other? (They actually did a lot of that in the Middle Ages). Are they geniuses whose activites are unfathomable for us normal people? Math is a very large field, but m

From playlist Summer of Math Exposition 2 videos

Direct sum

Related pages