
Semirings that are finite and have infinity
Semirings. You can find the simple python script here: https://gist.github.com/Nikolaj-K/f036fd07991fce26274b5b6f15a6c032 Previous video: https://youtu.be/ws6vCT7ExTY
From playlist Algebra

15 Properties of partially ordered sets
When a relation induces a partial ordering of a set, that set has certain properties with respect to the reflexive, (anti)-symmetric, and transitive properties.
From playlist Abstract algebra
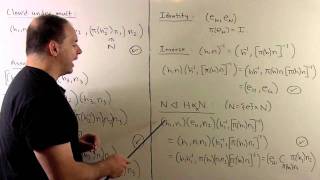
EDIT: At 6:24, the product should be "(e sub H, e sub N)", not "(e sub H, e sub G)" Abstract Algebra: Using automorphisms, we define the semidirect product of two groups. We prove the group property and construct various examples, including the dihedral groups. As an application, we
From playlist Abstract Algebra

Semisimple $\mathbb{Q}$-algebras in algebraic combinatorics by Allen Herman
PROGRAM GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fund
From playlist Group Algebras, Representations And Computation

Group automorphisms in abstract algebra
Group automorphisms are bijective mappings of a group onto itself. In this tutorial I define group automorphisms and introduce the fact that a set of such automorphisms can exist. This set is proven to be a subgroup of the symmetric group. You can learn more about Mathematica on my Udem
From playlist Abstract algebra

Representations of finite groups of Lie type (Lecture - 3) by Dipendra Prasad
PROGRAM GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fund
From playlist Group Algebras, Representations And Computation

Geometric Algebra - Rotors and Quaternions
In this video, we will take note of the even subalgebra of G(3), see that it is isomorphic to the quaternions and, in particular, the set of rotors, themselves in the even subalgebra, correspond to the set of unit quaternions. This brings the entire subject of quaternions under the heading
From playlist Math

Isomorphisms in abstract algebra
In this video I take a look at an example of a homomorphism that is both onto and one-to-one, i.e both surjective and injection, which makes it a bijection. Such a homomorphism is termed an isomorphism. Through the example, I review the construction of Cayley's tables for integers mod 4
From playlist Abstract algebra

Representation of finite groups over arbitrary fields by Ravindra S. Kulkarni
PROGRAM GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fund
From playlist Group Algebras, Representations And Computation

TQFTs from non-semisimple modular categories and modified traces, Marco de Renzi, Lecture II
Lecture series on modified traces in algebra and topology Topological Quantum Field Theories (TQFTs for short) provide very sophisticated tools for the study of topology in dimension 2 and 3: they contain invariants of 3-manifolds that can be computed by cut-and-paste methods, and their e
From playlist Lecture series on modified traces in algebra and topology

Anton Alekseev: Poisson-Lie duality and Langlands duality via Bohr-Sommerfeld
Abstract: Let G be a connected semisimple Lie group with Lie algebra 𝔤. There are two natural duality constructions that assign to it the Langlands dual group G^∨ (associated to the dual root system) and the Poisson-Lie dual group G^∗. Cartan subalgebras of 𝔤^∨ and 𝔤^∗ are isomorphic to ea
From playlist Topology

David Zywina, Computing Sato-Tate and monodromy groups.
VaNTAGe seminar on May 5, 2020. License: CC-BY-NC-SA Closed captions provided by Jun Bo Lau.
From playlist The Sato-Tate conjecture for abelian varieties

Group theory 7: Semidirect products
This is lecture 7 of an online course on group theory. It covers semidirect products and uses them to classify groups of order 6.
From playlist Group theory

TQFTs from non-semisimple modular categories and modified traces, Marco de Renzi, Lecture III
Lecture series on modified traces in algebra and topology Topological Quantum Field Theories (TQFTs for short) provide very sophisticated tools for the study of topology in dimension 2 and 3: they contain invariants of 3-manifolds that can be computed by cut-and-paste methods, and their e
From playlist Lecture series on modified traces in algebra and topology

Representation theory and geometry – Geordie Williamson – ICM2018
Plenary Lecture 17 Representation theory and geometry Geordie Williamson Abstract: One of the most fundamental questions in representation theory asks for a description of the simple representations. I will give an introduction to this problem with an emphasis on the representation theor
From playlist Plenary Lectures

The Lie-algebra of Quaternion algebras and their Lie-subalgebras
In this video we discuss the Lie-algebras of general quaternion algebras over general fields, especially as the Lie-algebra is naturally given for 2x2 representations. The video follows a longer video I previously did on quaternions, but this time I focus on the Lie-algebra operation. I st
From playlist Algebra

On the pioneering works of Professor I.B.S. Passi by Sugandha Maheshwari
PROGRAM GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fund
From playlist Group Algebras, Representations And Computation

Inner & Outer Semidirect Products Derivation - Group Theory
Semidirect products are a very important tool for studying groups because they allow us to break a group into smaller components using normal subgroups and complements! Here we describe a derivation for the idea of semidirect products and an explanation of how the map into the automorphism
From playlist Group Theory

The influence of the Luthar-Passi method on the study of units in group rings by Leo Margolis
PROGRAM GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fund
From playlist Group Algebras, Representations And Computation