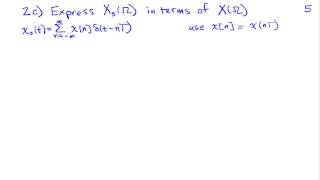Noise (electronics) | Signal processing
Quantization (signal processing)
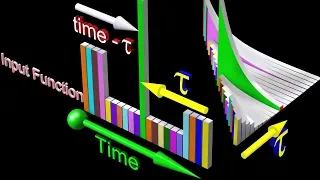
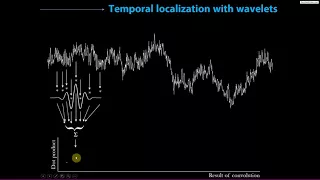
Quantization, in mathematics and digital signal processing, is the process of mapping input values from a large set (often a continuous set) to output values in a (countable) smaller set, often with a finite number of elements. Rounding and truncation are typical examples of quantization processes. Quantization is involved to some degree in nearly all digital signal processing, as the process of representing a signal in digital form ordinarily involves rounding. Quantization also forms the core of essentially all lossy compression algorithms. The difference between an input value and its quantized value (such as round-off error) is referred to as quantization error. A device or algorithmic function that performs quantization is called a quantizer. An analog-to-digital converter is an example of a quantizer. (Wikipedia).