
Introduction to Vector Fields This video discusses, 1) The definition of a vector field. 2) Examples of vector fields including the gradient, and various velocity fields. 3) The definition of a conservative vector field. 4) The definition of a potential function. 5) Test for conservative
From playlist Calculus 3

algebraic geometry 15 Projective space
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It introduces projective space and describes the synthetic and analytic approaches to projective geometry
From playlist Algebraic geometry I: Varieties

11_7_1 Potential Function of a Vector Field Part 1
The gradient of a function is a vector. n-Dimensional space can be filled up with countless vectors as values as inserted into a gradient function. This is then referred to as a vector field. Some vector fields have potential functions. In this video we start to look at how to calculat
From playlist Advanced Calculus / Multivariable Calculus

Multivariable Calculus | What is a vector field.
We introduce the notion of a vector field and give some graphical examples. We also define a conservative vector field with examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Multivariable Calculus

Introduction to Projective Geometry (Part 1)
The first video in a series on projective geometry. We discuss the motivation for studying projective planes, and list the axioms of affine planes.
From playlist Introduction to Projective Geometry
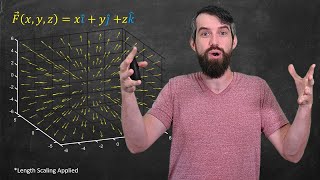
Intro to VECTOR FIELDS // Sketching by hand & with computers
Vector Fields are extremely important in math, physics, engineering, and many other fields. Gravitational fields, electric fields, magnetic fields, velocity fields, these are all examples of vector fields. In this video we will define the concept of a vector field, talk about some basic te
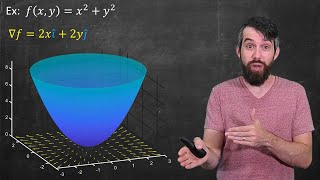
One prominent example of a vector field is the Gradient Vector Field. Given any scalar, multivariable function f: R^n\to R, we can get a corresponding vector field that has a precise geometrical meaning: the vectors point in the direction of maximal increase of the function. MY VECTOR CA

This video explains the definition of a vector space and provides examples of vector spaces.
From playlist Vector Spaces
The circle and projective homogeneous coordinates | Universal Hyperbolic Geometry 7a | NJ Wildberger
Universal hyperbolic geometry is based on projective geometry. This video introduces this important subject, which these days is sadly absent from most undergrad/college curriculums. We adopt the 19th century view of a projective space as the space of one-dimensional subspaces of an affine
From playlist Universal Hyperbolic Geometry

Branched Holomorphic Cartan Geometries by Sorin Dumitrescu
DISCUSSION MEETING ANALYTIC AND ALGEBRAIC GEOMETRY DATE:19 March 2018 to 24 March 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore. Complex analytic geometry is a very broad area of mathematics straddling differential geometry, algebraic geometry and analysis. Much of the interactions be
From playlist Analytic and Algebraic Geometry-2018

The flux as a line integral -- Calculus III
This lecture is on Calculus III. It follows Part III of the book Calculus Illustrated by Peter Saveliev. The text of the book can be found at http://calculus123.com.
From playlist Calculus III

Adolfo Guillot: Complete holomorphic vector fields and their singular points - lecture 2
CIRM VIRTUAL EVENT Recorded during the research school "Geometry and Dynamics of Foliations " the May 11, 2020 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on C
From playlist Virtual Conference

Verlinde Dimension Formula for the Space of Conformal Blocks and the moduli of G...V- Shrawan Kumar
Verlinde Dimension Formula Topic: Verlinde Dimension Formula for the Space of Conformal Blocks and the moduli of G-bundles V Speaker: Shrawan Kumar Affiliation: University of North Carolina; Member, School of Mathematics Date: November 17, 2022 Let G be a simply-connected complex semisim
From playlist Mathematics

To learn more about Wolfram Technology Conference, please visit: https://www.wolfram.com/events/technology-conference/ Speaker: José Martín-García Wolfram developers and colleagues discussed the latest in innovative technologies for cloud computing, interactive deployment, mobile devices
From playlist Wolfram Technology Conference 2018

Alessio Figalli, Fields medallist 2018 - International Meeting - 17 January 2019
https://www.sns.it/it/evento/alessio-figalli-fields-medallist-2018 Alessio Figalli, Fields medallist 2018 International Meeting This event gathers mathematicians that had a major role in Figalli’s career, either by inspiring and guiding him during his early stage, or by collaborating wit
From playlist Centro di Ricerca Matematica Ennio De Giorgi

Introduction to Projective Geometry (Part 3)
At long last! I'm rambling on about projective space again. Will it last? Who knows!?
From playlist Introduction to Projective Geometry

Holomorphic Cartan geometries on simply connected manifolds by Sorin Dumitrescu
Discussion Meeting Complex Algebraic Geometry ORGANIZERS: Indranil Biswas, Mahan Mj and A. J. Parameswaran DATE:01 October 2018 to 06 October 2018 VENUE: Madhava Lecture Hall, ICTS, Bangalore The discussion meeting on Complex Algebraic Geometry will be centered around the "Infosys-ICT
From playlist Complex Algebraic Geometry 2018

Nijenhuis geometry for ECRs: pre-recorded Lecture 1
Pre-recorded Lecture 1: Nijenhuis geometry for ECRs Date: 8 February 2022 Lecture slides: https://mathematical-research-institute.sydney.edu.au/wp-content/uploads/2022/02/Lecture-1_matveev.pdf -------------------------------------------------------------------------------------------------
From playlist MATRIX-SMRI Symposium: Nijenhuis Geometry and integrable systems

