Projective geometry | Incidence geometry
Oval (projective plane)
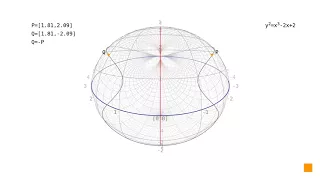
In projective geometry an oval is a point set in a plane that is defined by incidence properties. The standard examples are the nondegenerate conics. However, a conic is only defined in a pappian plane, whereas an oval may exist in any type of projective plane. In the literature, there are many criteria which imply that an oval is a conic, but there are many examples, both infinite and finite, of ovals in pappian planes which are not conics. As mentioned, in projective geometry an oval is defined by incidence properties, but in other areas, ovals may be defined to satisfy other criteria, for instance, in differential geometry by differentiability conditions in the real plane. The higher dimensional analog of an oval is an ovoid in a projective space. A generalization of the oval concept is an abstract oval, which is a structure that is not necessarily embedded in a projective plane. Indeed, there exist abstract ovals which can not lie in any projective plane. (Wikipedia).