Given the radius of a circle find the length of an arc
Learn how to solve problems with arcs of a circle. An arc is a curve made by two points on the circumference of a circle. The measure of an arc corresponds to the central angle made by the two radii from the center of the circle to the endpoints of the arc. The measure of the angle on a c
From playlist Circles

Learn to determine the length of an arc for a circle
Learn how to solve problems with arcs of a circle. An arc is a curve made by two points on the circumference of a circle. The measure of an arc corresponds to the central angle made by the two radii from the center of the circle to the endpoints of the arc. The measure of the angle on a c
From playlist Circles

What is the formula to determine the length of an arc
Learn how to solve problems with arcs of a circle. An arc is a curve made by two points on the circumference of a circle. The measure of an arc corresponds to the central angle made by the two radii from the center of the circle to the endpoints of the arc. The measure of the angle on a c
From playlist Circles

How to determine the measure of the arc if the chords are congruent
Learn how to solve problems with arcs of a circle. An arc is a curve made by two points on the circumference of a circle. The measure of an arc corresponds to the central angle made by the two radii from the center of the circle to the endpoints of the arc. The measure of the angle on a c
From playlist Circles
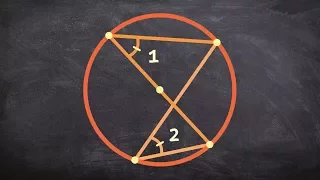
What is the relationship for two inscribed angles with the same endpoints
Learn how to solve problems with arcs of a circle. An arc is a curve made by two points on the circumference of a circle. The measure of an arc corresponds to the central angle made by the two radii from the center of the circle to the endpoints of the arc. The measure of the angle on a c
From playlist Circles
Find the length of a arc given the radius of a circle
Learn how to solve problems with arcs of a circle. An arc is a curve made by two points on the circumference of a circle. The measure of an arc corresponds to the central angle made by the two radii from the center of the circle to the endpoints of the arc. The measure of the angle on a c
From playlist Circles

What is the measure of the arc if two chords are congruent
Learn how to solve problems with arcs of a circle. An arc is a curve made by two points on the circumference of a circle. The measure of an arc corresponds to the central angle made by the two radii from the center of the circle to the endpoints of the arc. The measure of the angle on a c
From playlist Circles

What is the definition of a tangent line to a circle
Learn the essential definitions of the parts of a circle. A secant line to a circle is a line that crosses exactly two points on the circle while a tangent line to a circle is a line that touches exactly one point on the circle. A chord is a line that has its two endpoints on the circle.
From playlist Essential Definitions for Circles #Circles

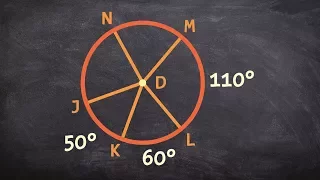
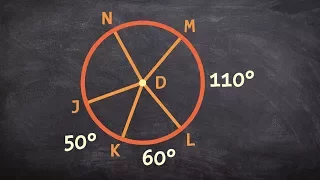
What is the sum of all central angles for a circle
Learn how to solve problems with arcs of a circle. An arc is a curve made by two points on the circumference of a circle. The measure of an arc corresponds to the central angle made by the two radii from the center of the circle to the endpoints of the arc. The measure of the angle on a c
From playlist Circles

Lecture 2: A structure theorem for rooted binary phylogenetic networks and its various applications
This video is one of the two introductory lectures (Introduction to Discrete Mathematical Biology) given by Momoko Hayamizu as part of an omnibus lecture series "Advanced Modern Mathematical Sciences 2" for undergraduate mathematics majors at Waseda University. In this lecture, she gives a
From playlist 2020 Advanced Topic in Modern Mathematical Sciences 2

Data Science with Mathematica -- Dynamic Programming
In this session of my Data Science with Mathematica track I provide an introduction to Dynamic Programming for the Data Scientist. DP is a very important, practical, flexible, and code-efficient way to solve problems in combinatorial optimization. Its applicability covers many fields: oper
From playlist Data Science with Mathematica

離散数学入門#11: マッチング(2):最大マッチングを見つける2つの方法
早稲田大学の全学部の3〜4年生を対象とする全学オープン科目「離散数学入門」(担当教員:早水 桃子)の授業動画です.文理を問わず,誰でもグラフ理論やグラフアルゴリズムの初歩を学ぶことができます.グラフ理論の定理やグラフに関するアルゴリズムを正しく理解して,現実の諸問題を解決するための応用力を身につけましょう. --------------------------------------------------------------------------------------- 最大マッチング問題は,なるべく多くのペアをマッチさせるようなマッチングを求める問題です.特に重
From playlist 離散数学入門Ⅳ

This video is about tournaments and some of their basic properties.
From playlist Basics: Graph Theory

Parabolic Splines and Archimedes | Algebraic Calculus One | Wild Egg
We introduce parabolic splines associated to the parabola with simple Cartesian equation y=x^2. We look at two different situations, first evaluating signed areas of polygonal spline approximations to bigger and bigger portions of the curve, and then to a closer and closer examination of j
From playlist Algebraic Calculus One from Wild Egg

Mariusz Mirek: Pointwise ergodic theorems for bilinear polynomial averages
We shall discuss the proof of pointwise almost everywhere convergence for the non-conventional (in the sense of Furstenberg and Weiss) bilinear polynomial ergodic averages. This is joint work with Ben Krause and Terry Tao: arXiv:2008.00857. We will also talk about recent progress towards e
From playlist Seminar Series "Harmonic Analysis from the Edge"

Solve for the value of x and y using congruent inscribed angles
Learn how to solve problems with arcs of a circle. An arc is a curve made by two points on the circumference of a circle. The measure of an arc corresponds to the central angle made by the two radii from the center of the circle to the endpoints of the arc. The measure of the angle on a c
From playlist Circles



