Monoidal category
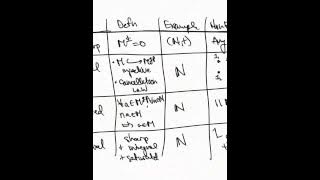
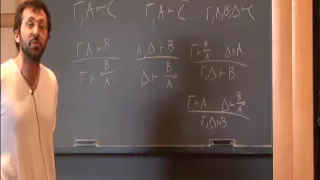
In mathematics, a monoidal category (or tensor category) is a category equipped with a bifunctor that is associative up to a natural isomorphism, and an object I that is both a left and right identity for ⊗, again up to a natural isomorphism. The associated natural isomorphisms are subject to certain coherence conditions, which ensure that all the relevant diagrams commute. The ordinary tensor product makes vector spaces, abelian groups, R-modules, or R-algebras into monoidal categories. Monoidal categories can be seen as a generalization of these and other examples. Every (small) monoidal category may also be viewed as a "categorification" of an underlying monoid, namely the monoid whose elements are the isomorphism classes of the category's objects and whose binary operation is given by the category's tensor product. A rather different application, of which monoidal categories can be considered an abstraction, is that of a system of data types closed under a type constructor that takes two types and builds an aggregate type; the types are the objects and is the aggregate constructor. The associativity up to isomorphism is then a way of expressing that different ways of aggregating the same data—such as and —store the same information even though the aggregate values need not be the same. The aggregate type may be analogous to the operation of addition (type sum) or of multiplication (type product). For type product, the identity object is the unit , so there is only one inhabitant of the type, and that is why a product with it is always isomorphic to the other operand. For type sum, the identity object is the void type, which stores no information and it is impossible to address an inhabitant. The concept of monoidal category does not presume that values of such aggregate types can be taken apart; on the contrary, it provides a framework that unifies classical and quantum information theory. In category theory, monoidal categories can be used to define the concept of a monoid object and an associated action on the objects of the category. They are also used in the definition of an enriched category. Monoidal categories have numerous applications outside of category theory proper. They are used to define models for the multiplicative fragment of intuitionistic linear logic. They also form the mathematical foundation for the topological order in condensed matter physics. Braided monoidal categories have applications in quantum information, quantum field theory, and string theory. (Wikipedia).