
Categories 6 Monoidal categories
This lecture is part of an online course on categories. We define strict monoidal categories, and then show how to relax the definition by introducing coherence conditions to define (non-strict) monoidal categories. We finish by defining symmetric monoidal categories and showing how super
From playlist Categories for the idle mathematician

Category Theory 10.2: Monoid in the category of endofunctors
Monad as a monoid in the category of endofunctors
From playlist Category Theory
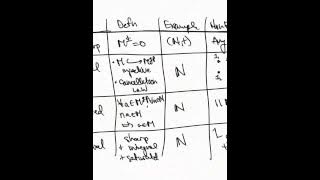
Geometry of Frobenioids - part 2 - (Set) Monoids
This is an introduction to the basic properties of Monoids. This video intended to be a starting place for log-schemes, Mochizuki's IUT or other absolute geometric constructions using monoids.
From playlist Geometry of Frobenioids

Higher Algebra 9: Symmetric monoidal infinity categories
In this video, we introduce the notion of a symmetric monoidal infinity categories and give some examples. Feel free to post comments and questions at our public forum at https://www.uni-muenster.de/TopologyQA/index.php?qa=tc-lecture Homepage with further information: https://www.uni-mu
From playlist Higher Algebra
Category theory for JavaScript programmers #24: monoidal functors
http://jscategory.wordpress.com/source-code/
From playlist Category theory for JavaScript programmers

Closed Intervals, Open Intervals, Half Open, Half Closed
00:00 Intro to intervals 00:09 What is a closed interval? 02:03 What is an open interval? 02:49 Half closed / Half open interval 05:58 Writing in interval notation
From playlist Calculus

Math 031 031017 Monotone Sequence Theorem
The rational numbers have holes: square root of 2 is irrational. Bounded sequences; bounded above, bounded below. Q. Does bounded imply convergent? (No.) Q. Does convergent imply bounded? (Yes.) Proof that convergent implies bounded. Statement of Monotone Sequence Theorem. Definition
From playlist Course 3: Calculus II (Spring 2017)

All About Closed Sets and Closures of Sets (and Clopen Sets) | Real Analysis
We introduced closed sets and clopen sets. We'll visit two definitions of closed sets. First, a set is closed if it is the complement of some open set, and second, a set is closed if it contains all of its limit points. We see examples of sets both closed and open (called "clopen sets") an
From playlist Real Analysis
Substructural Type Theory - Zeilberger
Noam Zeilberger IMDEA Software Institute; Member, School of Mathematics March 22, 2013 For more videos, visit http://video.ias.edu
From playlist Mathematics

Category theory for JavaScript programmers #27: string diagrams
http://jscategory.wordpress.com/source-code/
From playlist Category theory for JavaScript programmers

On the classification of fusion categories – Sonia Natale – ICM2018
Algebra Invited Lecture 2.5 On the classification of fusion categories Sonia Natale Abstract: We report, from an algebraic point of view, on some methods and results on the classification problem of fusion categories over an algebraically closed field of characteristic zero. © Interna
From playlist Algebra

Eugenia Cheng: "The periodic table of n-categories"
Speaker: Eugenia Cheng (University of Sheffield) Title: The periodic table of n-categories Event: Categories, Logic and Foundations of Physics IV (January 2009, Imperial College London) Slides: http://www.cs.ox.ac.uk/quantum/slides/clap4-eugeniacheng.pdf Abstract: Degenerate n-categories
From playlist Software Development Lectures

Sam Gunningham: Character stacks and (q−)geometric representation theory
Abstract: I will discuss applications of geometric representation theory to topological and quantum invariants of character stacks. In particular, I will explain how generalized Springer correspondence for class D-modules and Koszul duality for Hecke categories encode surprising structure
From playlist Algebraic and Complex Geometry
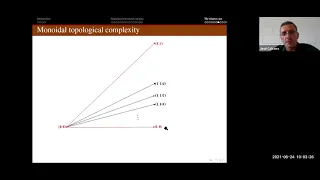
José Manuel García-Calcines (6/24/21): Topological complexity using arbitrary covers
Title: Topological complexity using arbitrary covers
From playlist Topological Complexity Seminar

Morgan Rogers - Toposes of Topological Monoid Actions
Talk at the school and conference “Toposes online” (24-30 June 2021): https://aroundtoposes.com/toposesonline/ Slides: https://aroundtoposes.com/wp-content/uploads/2021/07/RogersSlidesToposesOnline.pdf We explain the properties of the familiar properties of continuous actions of groups o
From playlist Toposes online

Lecture 7: Hochschild homology in ∞-categories
In this video, we construct Hochschild homology in an arbitrary symmetric-monoidal ∞-category. The most important special case is the ∞-category of spectra, in which we get Topological Hochschild homology. Feel free to post comments and questions at our public forum at https://www.uni-mu
From playlist Topological Cyclic Homology

Jack Morava: On the group completion of the Burau representation
Abstract: On fundamental groups, the discriminant ∏i≠k(zi – zk) ∈ C^× of a finite collection of points of the plane defines the abelianization homomorphism sending a braid to its number of overcrossings less undercrossings or writhe. In terms of diffeomorphisms of the punctured plane, it
From playlist SMRI Algebra and Geometry Online

Category Theory 2.2: Monomorphisms, simple types
Monomorphisms, simple types.
From playlist Category Theory
