
Andrey Gogolev: Rigidity in rank one: dynamics and geometry - lecture 1
A dynamical system is called rigid if a weak form of equivalence with a nearby system, such as coincidence of some simple invariants, implies a strong form of equivalence. In this minicourse we will discuss smooth rigidity of hyperbolic dynamical systems and related geometric questions suc
From playlist Dynamical Systems and Ordinary Differential Equations

Andrey Gogolev: Rigidity in rank one: dynamics and geometry - lecture 3
A dynamical system is called rigid if a weak form of equivalence with a nearby system, such as coincidence of some simple invariants, implies a strong form of equivalence. In this minicourse we will discuss smooth rigidity of hyperbolic dynamical systems and related geometric questions suc
From playlist Dynamical Systems and Ordinary Differential Equations

Andrey Gogolev: Rigidity in rank one: dynamics and geometry - lecture 2
A dynamical system is called rigid if a weak form of equivalence with a nearby system, such as coincidence of some simple invariants, implies a strong form of equivalence. In this minicourse we will discuss smooth rigidity of hyperbolic dynamical systems and related geometric questions suc
From playlist Dynamical Systems and Ordinary Differential Equations

Category Theory 3.1: Examples of categories, orders, monoids
Examples of categories, orders, monoids.
From playlist Category Theory

Categories 6 Monoidal categories
This lecture is part of an online course on categories. We define strict monoidal categories, and then show how to relax the definition by introducing coherence conditions to define (non-strict) monoidal categories. We finish by defining symmetric monoidal categories and showing how super
From playlist Categories for the idle mathematician

Normal Stress and Normal Strain | Mechanical Properties of Solids | Don't Memorise
Stress and strain are basically classified into two types of stress and types of strain: Normal Stress/ Normal Strain and Shear Stress/ Shear Strain. To know what they mean, watch the video! (Mechanical Properties of Solids) In this video, we will learn: 0:00 Introduction 0:09 Types of
From playlist Physics

Cohomologies for rigid analytic varieties via motivic homotopy theory by Alberto Vezzani
PERFECTOID SPACES ORGANIZERS: Debargha Banerjee, Denis Benois, Chitrabhanu Chaudhuri, and Narasimha Kumar Cheraku DATE & TIME: 09 September 2019 to 20 September 2019 VENUE: Madhava Lecture Hall, ICTS, Bangalore Scientific committee: Jacques Tilouine (University of Paris, France) Eknath
From playlist Perfectoid Spaces 2019

Cluster characters, generic bases for cluster algebras (Lecture 4) by Pierre-Guy Plamondon
PROGRAM :SCHOOL ON CLUSTER ALGEBRAS ORGANIZERS :Ashish Gupta and Ashish K Srivastava DATE :08 December 2018 to 22 December 2018 VENUE :Madhava Lecture Hall, ICTS Bangalore In 2000, S. Fomin and A. Zelevinsky introduced Cluster Algebras as abstractions of a combinatoro-algebra
From playlist School on Cluster Algebras 2018

Virtual rigid motives of definable sets in valued fields - A. Forey - Workshop 2 - CEB T1 2018
Arthur Forey (Sorbonne Université) / 08.03.2018 Virtual rigid motives of definable sets in valued fields. In an instance of motivic integration, Hrushovski and Kazhdan study the definable sets in the theory of algebraically closed valued fields of characteristic zero. They show that the
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

Title: On the Intermediate Singularities of the q-Difference Equations April 2016 Kolchin Seminar Workshop
From playlist April 2016 Kolchin Seminar Workshop

Konstantin Ardako - Equivariant D- modules on rigid analytic spaces
Séminaire Paris Pékin Tokyo / Mercredi 17 décembre 2014 Abstract : Given a curve over a dvr of mixed characteristic 0-p with smooth generic fiber and with semistable reduction, I will present a criterion for good reduction in terms of the (unipotent) p-adic étale fundamental group of its
From playlist Conférences Paris Pékin Tokyo

Flexibilization as localization - Oleg Lazarev
Workshop on the h-principle and beyond Topic: Flexibilization as localization Speaker: Oleg Lazarev Affiliation: University of Massachusetts, Boston Date: November 5, 2021 Abstract: Cieliebak and Eliashberg showed that there is a special class of flexible symplectic structures that sati
From playlist Mathematics

On the classification of fusion categories – Sonia Natale – ICM2018
Algebra Invited Lecture 2.5 On the classification of fusion categories Sonia Natale Abstract: We report, from an algebraic point of view, on some methods and results on the classification problem of fusion categories over an algebraically closed field of characteristic zero. © Interna
From playlist Algebra

Shuji Saito: Rigid analytic K theory
The lecture was held within the framework of the Hausdorff Trimester Program : Workshop "K-theory in algebraic geometry and number theory"
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"
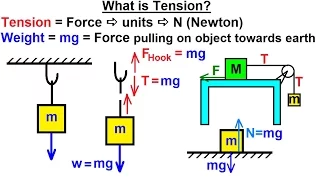
Physics - Mechanics: Ch 17 Tension and Weight (1 of 11) What is Tension?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is tension and how to calculate tension using the free-body diagram. Next video in this series can be seen at: https://youtu.be/BxUhaktD8PA
From playlist PHYSICS MECHANICS 1: INTRO, VECTORS, MOTION, PROJECTILE MOTION, NEWTON'S LAWS

Mirror symmetry for the mirror quartic, and other stories - Ivan Smith
Workshop on Homological Mirror Symmetry: Methods and Structures Speaker: Ivan Smith Topic: Mirror symmetry for the mirror quartic, and other stories Affiliation: University of Cambridge Date: November, 9, 2016 For more video, visit http://video.ias.edu
From playlist Workshop on Homological Mirror Symmetry: Methods and Structures

Periodic Classification of Elements - Introduction | Don't Memorise
Imagine you have to begin a library. And you have thousands of books of different genre. How would you arrange the books? Will you keep all the books together. Nope! For people to find the books of their interest easily you will arrange them in groups. Similarly, even in Chemistry, there a
From playlist Periodic Classification


