
B25 Example problem solving for a Bernoulli equation
See how to solve a Bernoulli equation.
From playlist Differential Equations

Solve a Bernoulli Differential Equation (Part 2)
This video provides an example of how to solve an Bernoulli Differential Equation. The solution is verified graphically. Library: http://mathispower4u.com
From playlist Bernoulli Differential Equations

Solve a Bernoulli Differential Equation (Part 1)
This video provides an example of how to solve an Bernoulli Differential Equation. The solution is verified graphically. Library: http://mathispower4u.com
From playlist Bernoulli Differential Equations

Solve a Bernoulli Differential Equation Initial Value Problem
This video provides an example of how to solve an Bernoulli Differential Equations Initial Value Problem. The solution is verified graphically. Library: http://mathispower4u.com
From playlist Bernoulli Differential Equations

C36 Example problem solving a Cauchy Euler equation
An example problem of a homogeneous, Cauchy-Euler equation, with constant coefficients.
From playlist Differential Equations

A06 Example problem including the Wronskian
Example problem solving a system of linear differential equations, including a look at the Wronskian so make sure that the solutions are not constant multiples of each other.
From playlist A Second Course in Differential Equations

Ex: Solve a Bernoulli Differential Equation Using an Integrating Factor
This video explains how to solve a Bernoulli differential equation. http://mathispower4u.com
From playlist Bernoulli Differential Equations

A Strange But Elegant Approach to a Surprisingly Hard Problem (GJK Algorithm)
In 1988, three engineers came together and developed one of the most clever solutions to the problem of detecting when two complex objects collide. Their solution, the Gilbert Johnson Keerthi (GJK) algorithm, named after the authors, made an incredible impact in the fields of robotics, con
From playlist Computer Graphics

Franz Schuster: Blaschke–Santaló Inequalities for Minkowski and Asplund Endomorphisms
The Blaschke–Santaló inequality is one of the best known and most powerful affine isoperimetric inequalities in convex geometric analysis. In particular, it is significantly stronger than the classical Euclidean Urysohn inequality. In this talk, we present new isoperimetric inequalities fo
From playlist Workshop: High dimensional measures: geometric and probabilistic aspects
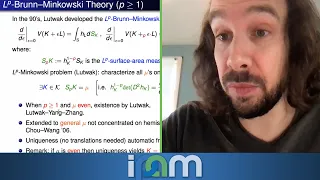
Emanuel Milman - The log-Minkowski Problem - IPAM at UCLA
Recorded 09 February 2022. Emanuel Milman of Technion - Israel Institute of Technology presents "The log-Minkowski Problem" at IPAM's Calculus of Variations in Probability and Geometry Workshop. Abstract: The classical Minkowski problem asks to find a convex body K in Rn having a prescrib
From playlist Workshop: Calculus of Variations in Probability and Geometry

Code - Seminar 28 - Ince on Robust and Fast Collision Detection in Games
Ince (https://twitter.com/Ince_FS) presents his new algorithm for fast and robust collision detection, using Minkowski differences. The webpage for this seminar is https://metauni.org/code/ You can join this seminar from anywhere, on any device, at https://www.metauni.org. This video wa
From playlist Code seminar

S.T. Yau - Geometry of spacetime and mass in general relativity [2018]
Slides for this talk: https://drive.google.com/open?id=1_WQg_5dgDIcUeO53NriLy79UZVFyHOzs Abstract: I shall discuss the role of geometry in creating the space time that is fundamental to the physics of general relativity. I shall also discuss fundamental concepts such as mass, linear momen
From playlist Mathematics

Embeddedness of timelike maximal surfaces in (1+2) Minkowski Space by Edmund Adam Paxton
Discussion Meeting Discussion meeting on zero mean curvature surfaces (ONLINE) Organizers: C. S. Aravinda and Rukmini Dey Date: 07 July 2020 to 15 July 2020 Venue: Online Due to the ongoing COVID-19 pandemic, the original program has been canceled. However, the meeting will be co
From playlist Discussion Meeting on Zero Mean Curvature Surfaces (Online)
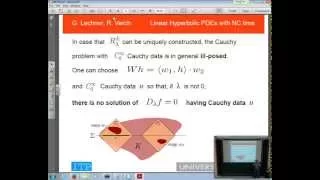
Rainer Verch: Linear hyperbolic PDEs with non-commutative time
Motivated by wave or Dirac equations on noncommutative deformations of Minkowski space, linear integro-differential equations of the form (D + sW) f = 0 are studied, where D is a normal or prenormal hyperbolic differential operator on Minkowski spacetime, s is a coupling constant, and W i
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

Tutorial for Juan Maldacena lectures by Yiming Chen
PROGRAM KAVLI ASIAN WINTER SCHOOL (KAWS) ON STRINGS, PARTICLES AND COSMOLOGY (ONLINE) ORGANIZERS Francesco Benini (SISSA, Italy), Bartek Czech (Tsinghua University, China), Dongmin Gang (Seoul National University, South Korea), Sungjay Lee (Korea Institute for Advanced Study, South Korea
From playlist Kavli Asian Winter School (KAWS) on Strings, Particles and Cosmology (ONLINE) - 2022

Jonathan Luk - A tale of two tails - IPAM at UCLA
Recorded 25 October 2021. Jonathan Luk of Stanford University presents "A tale of two tails" at IPAM's Workshop II: Mathematical and Numerical Aspects of Gravitation. Abstract: Motivated by the strong cosmic censorship conjecture, we study precise late-time tails for solutions to wave equa
From playlist Workshop: Mathematical and Numerical Aspects of Gravitation

C37 Example problem solving a Cauchy Euler equation
Example problem solving a homogeneous Cauchy-Euler equation.
From playlist Differential Equations

Sergiu Klainerman - 3/4 On the Mathematical Theory of Black Holes
https://indico.math.cnrs.fr/event/3463/ The gravitational waves detected by LIGO were produced in the final faze of the inward spiraling of two black holes before they collided to produce a more massive black hole. The experiment is entirely consistent with the so called Final State Conjec
From playlist Sergiu Klainerman - On the Mathematical Theory of Black Holes

C43 Example problem solving a Cauchy Euler equation
Another Cauchy-Euler equation example problem solved.
From playlist Differential Equations
