Miller index
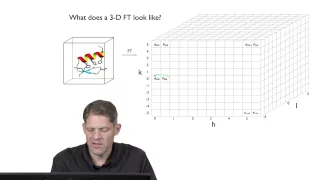
Miller indices form a notation system in crystallography for lattice planes in crystal (Bravais) lattices. In particular, a family of lattice planes of a given (direct) Bravais lattice is determined by three integers h, k, and ℓ, the Miller indices. They are written (hkℓ), and denote the family of (parallel) lattice planes (of the given Bravais lattice) orthogonal to , where are the basis or primitive translation vectors of the reciprocal lattice for the given Bravais lattice. (Note that the plane is not always orthogonal to the linear combination of direct or original lattice vectors because the direct lattice vectors need not be mutually orthogonal.) This is based on the fact that a reciprocal lattice vector (the vector indicating a reciprocal lattice point from the reciprocal lattice origin) is the wavevector of a plane wave in the Fourier series of a spatial function (e.g., electronic density function) which periodicity follows the original Bravais lattice, so wavefronts of the plane wave are coincident with parallel lattice planes of the original lattice. Since a measured scattering vector in X-ray crystallography, with as the outgoing (scattered from a crystal lattice) X-ray wavevector and as the incoming (toward the crystal lattice) X-ray wavevector, is equal to a reciprocal lattice vector as stated by the Laue equations, the measured scattered X-ray peak at each measured scattering vector is marked by Miller indices. By convention, negative integers are written with a bar, as in 3 for −3. The integers are usually written in lowest terms, i.e. their greatest common divisor should be 1. Miller indices are also used to designate reflections in X-ray crystallography. In this case the integers are not necessarily in lowest terms, and can be thought of as corresponding to planes spaced such that the reflections from adjacent planes would have a phase difference of exactly one wavelength (2π), regardless of whether there are atoms on all these planes or not. There are also several related notations: * the notation {hkℓ} denotes the set of all planes that are equivalent to (hkℓ) by the symmetry of the lattice. In the context of crystal directions (not planes), the corresponding notations are: * [hkℓ], with square instead of round brackets, denotes a direction in the basis of the direct lattice vectors instead of the reciprocal lattice; and * similarly, the notation denotes the set of all directions that are equivalent to [hkℓ] by symmetry. Note, for Laue-Bragg interferences * hkl lacks any bracketing when designating a reflection Miller indices were introduced in 1839 by the British mineralogist William Hallowes Miller, although an almost identical system (Weiss parameters) had already been used by German mineralogist Christian Samuel Weiss since 1817. The method was also historically known as the Millerian system, and the indices as Millerian, although this is now rare. The Miller indices are defined with respect to any choice of unit cell and not only with respect to primitive basis vectors, as is sometimes stated. (Wikipedia).