Ordinary differential equations
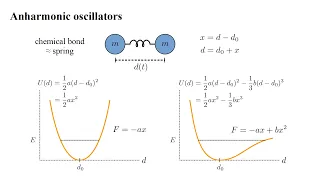
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force F proportional to the displacement x: where k is a positive constant. If F is the only force acting on the system, the system is called a simple harmonic oscillator, and it undergoes simple harmonic motion: sinusoidal oscillations about the equilibrium point, with a constant amplitude and a constant frequency (which does not depend on the amplitude). If a frictional force (damping) proportional to the velocity is also present, the harmonic oscillator is described as a damped oscillator. Depending on the friction coefficient, the system can: * Oscillate with a frequency lower than in the undamped case, and an amplitude decreasing with time (underdamped oscillator). * Decay to the equilibrium position, without oscillations (overdamped oscillator). The boundary solution between an underdamped oscillator and an overdamped oscillator occurs at a particular value of the friction coefficient and is called critically damped. If an external time-dependent force is present, the harmonic oscillator is described as a driven oscillator. Mechanical examples include pendulums (with small angles of displacement), masses connected to springs, and acoustical systems. Other include electrical harmonic oscillators such as RLC circuits. The harmonic oscillator model is very important in physics, because any mass subject to a force in stable equilibrium acts as a harmonic oscillator for small vibrations. Harmonic oscillators occur widely in nature and are exploited in many manmade devices, such as clocks and radio circuits. They are the source of virtually all sinusoidal vibrations and waves. (Wikipedia).