
What is the "spin" of a particle?
“Spin” is one of the core building blocks of quantum reality, but it is a subtle concept to grasp. Here’s Brian Greene with one way to think about it. Subscribe to our YouTube Channel for all the latest from World Science U. Visit our Website: http://www.worldscienceu.com/ Like us on Fac
From playlist Science Unplugged: Quantum Mechanics

Spin in quantum mechanics is an incredibly interesting property. However, it can be very difficult to understand what exactly it is. In this video, we dispel some misconceptions about spin as well as answer some of the more frequently asked questions about spin. #physics #quantum
From playlist Quantum Mechanics

Symmetric Groups (Abstract Algebra)
Symmetric groups are some of the most essential types of finite groups. A symmetric group is the group of permutations on a set. The group of permutations on a set of n-elements is denoted S_n. Symmetric groups capture the history of abstract algebra, provide a wide range of examples in
From playlist Abstract Algebra

Group Theory: The Center of a Group G is a Subgroup of G Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Group Theory: The Center of a Group G is a Subgroup of G Proof
From playlist Abstract Algebra

You've Heard of SPIN - But How Is it Encoded in the Math of Quantum Physics? Parth G
The concept of Spin is hard, but the mathematics is actually quite simple! In this video I wanted to take a look at how we build up our mathematical representation (or at least one of them) of quantum mechanical spin. To do this, we'll start by looking at the spin of an electron, and unde
From playlist Quantum Physics by Parth G

How did the concept of particles having "spin" arise from experimental studies?
Subscribe to our YouTube Channel for all the latest from World Science U. Visit our Website: http://www.worldscienceu.com/ Like us on Facebook: https://www.facebook.com/worldscienceu Follow us on Twitter: https://twitter.com/worldscienceu
From playlist Science Unplugged: Quantum Mechanics
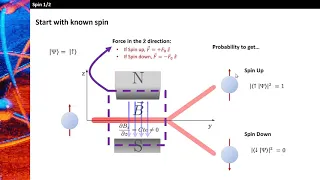
We briefly discuss the spin of particles in the z-direction in the language of Dirac Notation, and introduce the Stern-Gerlach experiment and its role in making measurements of spin.
From playlist Quantum Mechanics Uploads

Spin in Quantum Mechanics: What Is It and Why Are Electrons Spin 1/2? Physics Basics
The first 1000 people to use the link in my description will get a free trial of Skillshare Premium Membership: https://skl.sh/parthg11201 Hey everyone, I'm back with a new video! In this episode of "Quantum Mechanics, But Quickly", we're looking at the basics of Spin! Spin is a very int
From playlist Quantum Physics by Parth G

The Special Linear Group is a Subgroup of the General Linear Group Proof
The Special Linear Group is a Subgroup of the General Linear Group Proof
From playlist Abstract Algebra

Chem 125. Advanced Organic Chemistry. 26. Spin-Spin Coupling in 1H NMR Spectroscopy.
UCI Chem 125 Advanced Organic Chemistry (Spring 2016) Chem 125. Advanced Organic Chemistry. 26. Spin-Spin Coupling in 1H NMR Spectroscopy. View the complete course: http://ocw.uci.edu/courses/chem_125_advanced_organic_chemistry.html Instructor: James S. Nowick, Ph.D. License: Creat
From playlist Chem125: Advanced Organic Chemistry

Chem 203. Lecture 12: Magnetic Equivalence, Spin Systems, and Pople Notation
Full Chem 203 Playlist: https://www.youtube.com/playlist?list=PLqOZ6FD_RQ7nUiPCa47zSrMWArKAdwfcD UCI Chem 203 Organic Spectroscopy (Fall 2020) Lecture 12: Magnetic Equivalence, Spin Systems, and Pople Notation Instructor: James S. Nowick, Ph.D. License: Creative Commons BY-NC-SA Terms of
From playlist Chemistry 203, Organic Spectroscopy (2020)

Johannes Ebert - Rigidity theorems for the diffeomorphism action on spaces of metrics of (...)
The diffeomorphism group $\mathrm{Diff}(M)$ of a closed manifold acts on the space $\mathcal{R}^+ (M)$ of positive scalar curvature metrics. For a basepoint $g$, we obtain an orbit map $\sigma_g: \mathrm{Diff}(M) \to \mathcal{R}^ (M)$ which induces a map $(\sigma_g)_*:\pi_*( \mathrm{Diff}(
From playlist Not Only Scalar Curvature Seminar
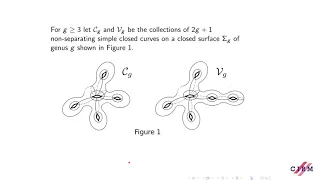
Ursula Hamenstädt: Spin mapping class groups and curve graphs
CIRM VIRTUAL EVENT Recorded during the meeting"Virtual Geometric Group Theory conference " the May 21, 2020 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM
From playlist Virtual Conference

Yanli Song: K-theory of the reduced C*-algebra of a real reductive Lie group
Talk by Yanli Song in Global Noncommutative Geometry Seminar (Americas) on January 28, 2022 in https://globalncgseminar.org/talks/tba-23/
From playlist Global Noncommutative Geometry Seminar (Americas)

Distiguished Lecture Series by Richard Melrose (Massachusetts Institute of Technology, USA)
From playlist Distinguished Visitors Lecture Series

Chem 203 Lecture 11: NMR Chemical Shifts, Chemical Equivalence, and Spin Spin Coupling
Full Chem 203 Playlist: https://www.youtube.com/playlist?list=PLqOZ6FD_RQ7nUiPCa47zSrMWArKAdwfcD UCI Chem 203 Organic Spectroscopy (Fall 2020) Lecture 11: NMR Chemical Shifts, Chemical Equivalence, and Spin Spin Coupling Instructor: James S. Nowick, Ph.D. License: Creative Commons BY-NC-S
From playlist Chemistry 203, Organic Spectroscopy (2020)

Chem 203. Organic Spectroscopy. Lecture 11. Magnetic Equivalence, Spin Systems, and Pople Notation
UCI Chem 203 Organic Spectroscopy (Fall 2011) Lec 11. Organic Spectroscopy -- Magnetic Equivalence, Spin Systems, and Pople Notation. View the complete course: http://ocw.uci.edu/courses/chem_203_organic_spectroscopy.html Instructor: James Nowick, Ph.D. License: Creative Commons BY-NC-SA
From playlist Chem 203: Organic Spectroscopy

Lecture 4 | New Revolutions in Particle Physics: Standard Model
(February 1, 2010) Professor Leonard Susskind continues his discussion of group theory. This course is a continuation of the Fall quarter on particle physics. The material will focus on the Standard Model of particle physics, especially quantum chromodynamics (the theory of quarks) and th
From playlist Lecture Collection | Particle Physics: Standard Model

Jonathan Rosenberg: Positive scalar curvature on a class of spin pseudomanifolds.
Talk by Jonathan Rosenberg in Global Noncommutative Geometry Seminar (Americas) http://www.math.wustl.edu/~xtang/NCG-Seminar on April 22, 2020.
From playlist Global Noncommutative Geometry Seminar (Americas)

Now that we know what a quotient group is, let's take a look at an example to cement our understanding of the concepts involved.
From playlist Abstract algebra