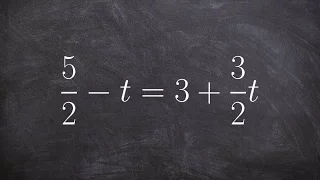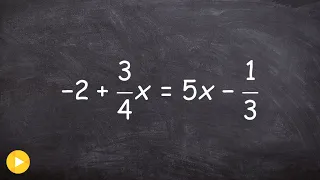Duodecimal
The duodecimal system (also known as base 12, dozenal, or, rarely, uncial) is a positional notation numeral system using twelve as its base. The number twelve (that is, the number written as "12" in the decimal numerical system) is instead written as "10" in duodecimal (meaning "1 dozen and 0 units", instead of "1 ten and 0 units"), whereas the digit string "12" means "1 dozen and 2 units" (decimal 14). Similarly, in duodecimal, "100" means "1 gross", "1000" means "1 great gross", and "0.1" means "1 twelfth" (instead of their decimal meanings "1 hundred", "1 thousand", and "1 tenth", respectively). Various symbols have been used to stand for ten and eleven in duodecimal notation; this page uses A and B, as in hexadecimal, which make a duodecimal count from zero to twelve read 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, 10. The Dozenal Societies of America and Great Britain (organisations promoting the use of duodecimal) use turned digits in their published material: ↊ (a turned 2) for ten and ↋ (a turned 3) for eleven. The number twelve, a superior highly composite number, is the smallest number with four non-trivial factors (2, 3, 4, 6), and the smallest to include as factors all four numbers (1 to 4) within the subitizing range, and the smallest abundant number. All multiples of reciprocals of 3-smooth numbers (a/2b·3c where a,b,c are integers) have a terminating representation in duodecimal. In particular, +1⁄4 (0.3), +1⁄3 (0.4), +1⁄2 (0.6), +2⁄3 (0.8), and +3⁄4 (0.9) all have a short terminating representation in duodecimal. There is also higher regularity observable in the duodecimal multiplication table. As a result, duodecimal has been described as the optimal number system. In these respects, duodecimal is considered superior to decimal (which has only 2 and 5 as factors) and other proposed bases like octal or hexadecimal. Sexagesimal does even better in this respect (the reciprocals of all 5-smooth numbers terminate), but at the cost of unwieldy multiplication tables and a much larger number of symbols to memorize. (Wikipedia).