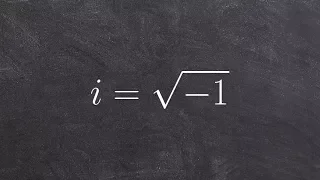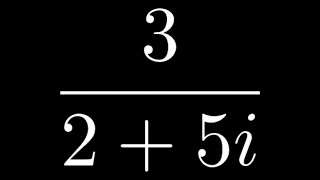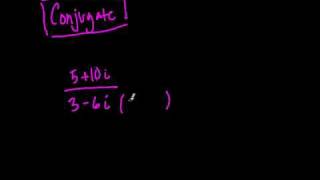Mathematics of music | Integer sequences
Regular number
Regular numbers are numbers that evenly divide powers of 60 (or, equivalently, powers of 30). Equivalently, they are the numbers whose only prime divisors are 2, 3, and 5. As an example, 602 = 3600 = 48 × 75, so as divisors of a power of 60 both 48 and 75 are regular. These numbers arise in several areas of mathematics and its applications, and have different names coming from their different areas of study. * In number theory, these numbers are called 5-smooth, because they can be characterized as having only 2, 3, or 5 as their prime factors. This is a specific case of the more general k-smooth numbers, the numbers that have no prime factor greater than k. * In the study of Babylonian mathematics, the divisors of powers of 60 are called regular numbers or regular sexagesimal numbers, and are of great importance in this area because of the sexagesimal (base 60) number system that the Babylonians used for writing their numbers, and that was central to Babylonian mathematics. * In music theory, regular numbers occur in the ratios of tones in five-limit just intonation. In connection with music theory and related theories of architecture, these numbers have been called the harmonic whole numbers. * In computer science, regular numbers are often called Hamming numbers, after Richard Hamming, who proposed the problem of finding computer algorithms for generating these numbers in ascending order. This problem has been used as a test case for functional programming. (Wikipedia).