
When is a Physical Quantity Conserved in Quantum Mechanics?
It is always interesting to know whether there are quantities in a physical system that are constant over time, so-called conserved quantities. In this video, we will explore the condition for whether a quantity is conserved and what this has to do with the Hamiltonian of the system. Ref
From playlist Quantum Mechanics, Quantum Field Theory

8 AWESOME EXAMPLES Conservation of angular momentum!!!
In this video you can see eight different examples Conservation of angular momentum. Also i explain that the angular momentum of a system will be conserved as long as there is no net external torque. Both point objects and extended objects are covered along with several examples.
From playlist MECHANICS

What Is The Law of Conservation of Mass | Properties of Matter | Chemistry | FuseSchool
Learn the basics about the law of the conservation of mass, when learning about properties of matter. The Law of Conservation of Mass says that in chemical reactions no matter is lost or gained. The law of conservation of mass means that during chemical change there is no loss or gain o
From playlist CHEMISTRY

Law of Conservation of Mass - Fundamental Chemical Laws, Chemistry
This chemistry video tutorial discusses the law of conservation of mass and provides examples associated with chemical reactions. The conservation of mass in a chemical reaction is one of the fundamental laws in chemistry. The total mass of the reactants must equal the total mass of the
From playlist New AP & General Chemistry Video Playlist

First example of using a symmetry principle show a conserved quantity. I show that the conservation of linear momentum comes from a radial symmetry in forces.
From playlist Physics ONE

A clip used to illustrate conservation of momentum
From playlist Mechanics, Elasticity, Fluids, Diffusion
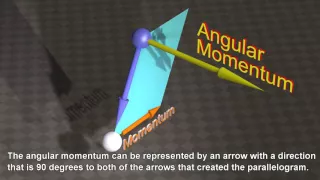
Momentum and Angular Momentum of the Universe
Visualization of the conservation of the momentum and angular momentum of everything in the universe.
From playlist Physics

Teach Astronomy - Conservation of Energy
http://www.teachastronomy.com/ One of the most important principles in physics is the law of conservation of energy. Energy can be neither created nor destroyed. In any closed physical system the total amount of energy is constant, although the energy may change forms multiple times. Wh
From playlist 04. Chemistry and Physics

Making YOU the Scientist: Density of Liquids
This a fun experiment that can be done in almost any setting: in the classroom, during home schooling, as an online learning demonstration or just a fun thing to do with the kids on the weekend. Everything you need you probably have around the house or you can get it with a quick trip to t
From playlist Making You the Scientist

Noether Networks: Meta-Learning Useful Conserved Quantities (w/ the authors)
#deeplearning #noether #symmetries This video includes an interview with first author Ferran Alet! Encoding inductive biases has been a long established methods to provide deep networks with the ability to learn from less data. Especially useful are encodings of symmetry properties of the
From playlist Papers Explained

3/4-Fractional superdiffusion in a system of harmonic oscillators... - Cédric Bernardin
Cédric Bernardin Université Nice Sophia Antipolis February 18, 2014 We consider an harmonic chain perturbed by an energy conserving noise and show that after a space-time rescaling the energy-energy correlation function is given by the solution of a skew-fractional heat equation with expon
From playlist Mathematics

Lecture 5 | Modern Physics: Special Relativity (Stanford)
Lecture 5 of Leonard Susskind's Modern Physics course concentrating on Special Relativity. Recorded May 12, 2008 at Stanford University. This Stanford Continuing Studies course is the first of a six-quarter sequence of classes exploring the essential theoretical foundations of modern ph
From playlist Lecture Collection | Modern Physics: Special Relativity

Hydrodynamics, variational principles and integrability (Pedagogical Lecture 1) by Alexander Abanov
PROGRAM: INTEGRABLE SYSTEMS IN MATHEMATICS, CONDENSED MATTER AND STATISTICAL PHYSICS ORGANIZERS: Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE : 16 July 2018 to 10 August 2018 VENUE: Ramanujan Lecture Hall, ICTS Bangalore
From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics

Your Daily Equation #25: Noether's Amazing Theorem: Symmetry and Conservation
Episode 25 #YourDailyEquation: In 1918, the phenomenal German mathematician Emmy Noether discovered a deep link between symmetries and conserved quantities, which has proven to be one of the most influential mathematical results in the development of physical laws. Join Brian Greene for an
From playlist Your Daily Equation with Brian Greene

Kolmogorov theory of homogeneous isotropic turbulence... ( Part 2) by J K Bhattacharjee
Summer school and Discussion Meeting on Buoyancy-driven flows DATE: 12 June 2017 to 20 June 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru Buoyancy plays a major role in the dynamics of atmosphere and interiors of planets and stars, as well as in engineering applications. This field
From playlist Summer school and Discussion Meeting on Buoyancy-driven flows

Lecture 1 | Modern Physics: Statistical Mechanics
March 30, 2009 - Leonard Susskind discusses the study of statistical analysis as calculating the probability of things subject to the constraints of a conserved quantity. Susskind introduces energy, entropy, temperature, and phase states as they relate directly to statistical mechanics.
From playlist Lecture Collection | Modern Physics: Statistical Mechanics

Thermal diffusion and energy transport for system.. by Stefano Olla
PROGRAM THERMALIZATION, MANY BODY LOCALIZATION AND HYDRODYNAMICS ORGANIZERS: Dmitry Abanin, Abhishek Dhar, François Huveneers, Takahiro Sagawa, Keiji Saito, Herbert Spohn and Hal Tasaki DATE : 11 November 2019 to 29 November 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore How do is
From playlist Thermalization, Many Body Localization And Hydrodynamics 2019

Geometric Algebra Applications - Kepler Problem (Part 2)
In this video, we show that the trajectories of masses moving under an inverse-square law are conic sections using geometric algebra. We will not be solving any differential equations, but instead showing that a special vector, the Laplace-Runge-Lenz vector, is a conserved quantity of moti
From playlist Math

A Package for Symbolic PDE Analysis
To learn more about Wolfram Technology Conference, please visit: https://www.wolfram.com/events/technology-conference/ Speaker: Davit Shahnazaryan Wolfram developers and colleagues discussed the latest in innovative technologies for cloud computing, interactive deployment, mobile devices
From playlist Wolfram Technology Conference 2017

Momentum (1 of 16) An Explanation
This video gives a complete explanation of momentum. It also includes an example momentum problem. Momentum is a quantity of matter arising from its mass and velocity. The momentum of an object is directly proportional to its mass and velocity. Momentum is a vector quantity. Impulse is th
From playlist Momentum, Impulse, Inelastic and Elastic Collisions