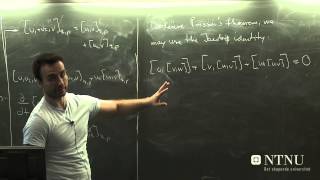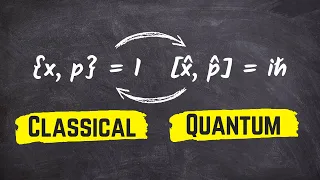Bilinear maps | Symplectic geometry | Hamiltonian mechanics
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time evolution of a Hamiltonian dynamical system. The Poisson bracket also distinguishes a certain class of coordinate transformations, called canonical transformations, which map canonical coordinate systems into canonical coordinate systems. A "canonical coordinate system" consists of canonical position and momentum variables (below symbolized by and , respectively) that satisfy canonical Poisson bracket relations. The set of possible canonical transformations is always very rich. For instance, it is often possible to choose the Hamiltonian itself as one of the new canonical momentum coordinates. In a more general sense, the Poisson bracket is used to define a Poisson algebra, of which the algebra of functions on a Poisson manifold is a special case. There are other general examples, as well: it occurs in the theory of Lie algebras, where the tensor algebra of a Lie algebra forms a Poisson algebra; a detailed construction of how this comes about is given in the universal enveloping algebra article. Quantum deformations of the universal enveloping algebra lead to the notion of quantum groups. All of these objects are named in honor of Siméon Denis Poisson. (Wikipedia).