Complex affine space

Complex manifolds

Affine geometry, broadly speaking, is the study of the geometrical properties of lines, planes, and their higher dimensional analogs, in which a notion of "parallel" is retained, but no metrical notions of distance or angle are. Affine spaces differ from linear spaces (that is, vector spaces) in that they do not have a distinguished choice of origin. So, in the words of Marcel Berger, "An affine space is nothing more than a vector space whose origin we try to forget about, by adding translations to the linear maps." Accordingly, a complex affine space, that is an affine space over the complex numbers, is like a complex vector space, but without a distinguished point to serve as the origin. Affine geometry is one of the two main branches of classical algebraic geometry, the other being projective geometry. A complex affine space can be obtained from a complex projective space by fixing a hyperplane, which can be thought of as a hyperplane of ideal points "at infinity" of the affine space. To illustrate the difference (over the real numbers), a parabola in the affine plane intersects the line at infinity, whereas an ellipse does not. However, any two conic sections are projectively equivalent. So a parabola and ellipse are the same when thought of projectively, but different when regarded as affine objects. Somewhat less intuitively, over the complex numbers, an ellipse intersects the line at infinity in a pair of points while a parabola intersects the line at infinity in a single point. So, for a slightly different reason, an ellipse and parabola are inequivalent over the complex affine plane but remain equivalent over the (complex) projective plane. Any complex vector space is an affine space: all one needs to do is forget the origin (and possibly any additional structure such as an inner product). For example, the complex n-space can be regarded as a complex affine space, when one is interested only in its affine properties (as opposed to its linear or metrical properties, for example). Since any two affine spaces of the same dimension are isomorphic, in some situations it is appropriate to identify them with , with the understanding that only affinely-invariant notions are ultimately meaningful. This usage is very common in modern algebraic geometry. (Wikipedia).

algebraic geometry 5 Affine space and the Zariski topology

This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It covers the definition of affine space and its Zariski topology.

From playlist Algebraic geometry I: Varieties

algebraic geometry 17 Affine and projective varieties

This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It covers the relation between affine and projective varieties, with some examples such as a cubic curve and the twisted cubic.

From playlist Algebraic geometry I: Varieties

algebraic geometry 15 Projective space

This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It introduces projective space and describes the synthetic and analytic approaches to projective geometry

From playlist Algebraic geometry I: Varieties

Definition of Vector Space

The formal definition of a vector space.

From playlist Linear Algebra Done Right

A WEIRD VECTOR SPACE: Building a Vector Space with Symmetry | Nathan Dalaklis

We'll spend time in this video on a weird vector space that can be built by developing the ideas around symmetry. In the process of building a vector space with symmetry at its core, we'll go through a ton of different ideas across a handful of mathematical fields. Naturally, we will start

From playlist The New CHALKboard

What are complex numbers? | Essence of complex analysis #2

A complete guide to the basics of complex numbers. Feel free to pause and catch a breath if you feel like it - it's meant to be a crash course! Complex numbers are useful in basically all sorts of applications, because even in the real world, making things complex sometimes, oxymoronicall

From playlist Essence of complex analysis

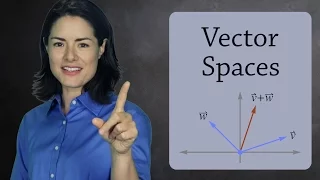
What is a Vector Space? (Abstract Algebra)

Vector spaces are one of the fundamental objects you study in abstract algebra. They are a significant generalization of the 2- and 3-dimensional vectors you study in science. In this lesson we talk about the definition of a vector space and give a few surprising examples. Be sure to su

From playlist Abstract Algebra

From Cohomology to Derived Functors by Suresh Nayak

PROGRAM DUALITIES IN TOPOLOGY AND ALGEBRA (ONLINE) ORGANIZERS: Samik Basu (ISI Kolkata, India), Anita Naolekar (ISI Bangalore, India) and Rekha Santhanam (IIT Mumbai, India) DATE & TIME: 01 February 2021 to 13 February 2021 VENUE: Online Duality phenomena are ubiquitous in mathematics

From playlist Dualities in Topology and Algebra (Online)

Holomorphic rigid geometric structures on compact manifolds by Sorin Dumitrescu

Higgs bundles URL: http://www.icts.res.in/program/hb2016 DATES: Monday 21 Mar, 2016 - Friday 01 Apr, 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore DESCRIPTION: Higgs bundles arise as solutions to noncompact analog of the Yang-Mills equation. Hitchin showed that irreducible solutio

From playlist Higgs Bundles

Complex Numbers as Points (1 of 4: Geometric Meaning of Addition)

More resources available at www.misterwootube.com

From playlist Complex Numbers

algebraic geometry 29 Automorphisms of space

This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It describes the automorphisms of affine and projective space, and gives a brief discussion of the Jacobian conjecture.

From playlist Algebraic geometry I: Varieties

Duality in Algebraic Geometry by Suresh Nayak

From playlist Dualities in Topology and Algebra (Online)

Mad Max: Affine spline insights into deep learning - Richard Baraniuk, Rice University

This workshop - organised under the auspices of the Isaac Newton Institute on “Approximation, sampling and compression in data science” — brings together leading researchers in the general fields of mathematics, statistics, computer science and engineering. About the event The workshop ai

From playlist Mathematics of data: Structured representations for sensing, approximation and learning

A Gentle Approach to Crystalline Cohomology - Jacob Lurie

Members’ Colloquium Topic: A Gentle Approach to Crystalline Cohomology Speaker: Jacob Lurie Affiliation: Professor, School of Mathematics Date: February 28, 2022 Let X be a smooth affine algebraic variety over the field C of complex numbers (that is, a smooth submanifold of C^n which can

From playlist Mathematics

Grothendieck-Serre Duality by Suresh Nayak

From playlist Dualities in Topology and Algebra (Online)

Complex Numbers as Vectors (2 of 3: Subtraction)

More resources available at www.misterwootube.com

From playlist Complex Numbers

algebraic geometry 20 Grassmannians

This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It is about Grassmannians and some of their applications.

From playlist Algebraic geometry I: Varieties

What is the complex conjugate?

What is the complex conjugate of a complex number? Free ebook http://bookboon.com/en/introduction-to-complex-numbers-ebook

From playlist Intro to Complex Numbers

Nexus Trimester - Alexandre d'Aspremont (École Normale Supérieure)

An Optimal Affine Invariant Smooth Minimization Algorithm Alexandre d'Aspremont (École Normale Supérieure) March 18, 2016 Abstract: We formulate an affine invariant implementation of the algorithm in (Nesterov, 1983). We show that the complexity bound is then proportional to an affine in

From playlist 2016-T1 - Nexus of Information and Computation Theory - CEB Trimester

Complex affine space

Related pages