
Présentation de l'exposition "Emile Borel : un mathématicien au pluriel"
---------------------------------- Institut Henri Poincaré, 11 rue Pierre et Marie Curie, 75005 PARIS http://www.ihp.fr/ Rejoignez les réseaux sociaux de l'IHP pour être au courant de nos actualités : - Facebook : https://www.facebook.com/InstitutHenriPoincare/ - Twitter : https://twitter
From playlist Bibliothèque

Here I prove the Heine-Borel Theorem, one of the most fundamental theorems in analysis. It says that in R^n, all boxes must be compact. The proof itself is very neat, and uses a bisection-type argument. Enjoy! Topology Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmA13vj9xkHG
From playlist Topology

Emile Borel: Real number enthusiast or skeptic? | Sociology and Pure Mathematics | N J Wildberger
Emile Borel was a prominent French analyst and probabilist, and the founder of modern measure theory. He was also involved in the issue of "real numbers" and just what they actually are, and what it means to do arithmetic with them. This is a first introduction to his thinking, where we d
From playlist Sociology and Pure Mathematics

What is the Riemann Hypothesis?
This video provides a basic introduction to the Riemann Hypothesis based on the the superb book 'Prime Obsession' by John Derbyshire. Along the way I look at convergent and divergent series, Euler's famous solution to the Basel problem, and the Riemann-Zeta function. Analytic continuation
From playlist Mathematics

Ptolemy's theorem and generalizations | Rational Geometry Math Foundations 131 | NJ Wildberger
The other famous classical theorem about cyclic quadrilaterals is due to the great Greek astronomer and mathematician, Claudius Ptolemy. Adopting a rational point of view, we need to rethink this theorem to state it in a purely algebraic way, without resort to `distances' and the correspon
From playlist Math Foundations
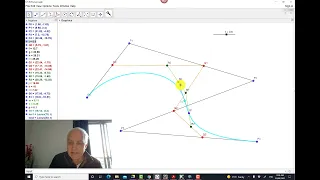
Polynumbers and de Casteljau Bezier curves | Algebraic Calculus and dCB curves | N J Wildberger
The Algebraic Calculus is an exciting new approach to calculus, not reliant on "infinite processes" and "real numbers". The central objects are polynomially parametrized curve, which turn out to be the same as the de Casteljau Bezier curves which play such a big role in design, animation,
From playlist Algebraic Calculus One Info

What are Hyperbolas? | Ch 1, Hyperbolic Trigonometry
This is the first chapter in a series about hyperbolas from first principles, reimagining trigonometry using hyperbolas instead of circles. This first chapter defines hyperbolas and hyperbolic relationships and sets some foreshadowings for later chapters This is my completed submission t
From playlist Summer of Math Exposition 2 videos

Stavros Garoufalidis - Arithmetic Resurgence of Quantum Invariants
I will explain some conjectures concerning arithmetic resurgence of quantum knot and 3-manifold invariants formulated in an earlier work of mine in 2008, as well as numerical tests of those conjectures and their relations to quantum modular forms, state integrals and their q-series. Joint
From playlist Resurgence in Mathematics and Physics

My joint work with Armand Borel from 1952-1954 - Frederich Hirzebruch
75th Anniversary Celebration School of Mathematics Frederich Hirzebruch Bonn University March 12, 2005 More videos on http://video.ias.edu
From playlist Mathematics

Differential Isomorphism and Equivalence of Algebraic Varieties Board at 49:35 Sum_i=1^N 2/(x-phi_i(y,t))^2
From playlist Fall 2017

Borel-Cantelli Lemmas for Inhomogeneous Diophantine Approximations and beyond by Victor Beresnevich
PROGRAM : ERGODIC THEORY AND DYNAMICAL SYSTEMS (HYBRID) ORGANIZERS : C. S. Aravinda (TIFR-CAM, Bengaluru), Anish Ghosh (TIFR, Mumbai) and Riddhi Shah (JNU, New Delhi) DATE : 05 December 2022 to 16 December 2022 VENUE : Ramanujan Lecture Hall and Online The programme will have an emphasis
From playlist Ergodic Theory and Dynamical Systems 2022

Boris Adamczewski : Aléa, automates et transcendance
HYBRID EVENT L'étude du caractère aléatoire de la suite des chiffres de certains nombres réels donne lieu à des problèmes classiques, comme la conjecture de normalité des nombres algébriques ou la conjecture de dimensions de Furstenberg (1969). Malheureusement, notre capacité à les appréhe
From playlist Combinatorics

Christoph Winges: Automorphisms of manifolds and the Farrell Jones conjectures
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Building on previous work of Bartels, Lück, Reich and others studying the algebraic K-theory and L-theory of discrete group rings, the validity of the Farrell-Jones Conjecture has be
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Kęstutis Česnavičius - Grothendieck–Serre in the quasi-split unramified case
Correction: The affiliation of Lei Fu is Tsinghua University. The Grothendieck–Serre conjecture predicts that every generically trivial torsor under a reductive group scheme G over a regular local ring R is trivial. We settle it in the case when G is quasi-split and R is unramified. To ov
From playlist Conférence « Géométrie arithmétique en l’honneur de Luc Illusie » - 5 mai 2021

An explicit supercuspidal local Langlands correspondence - Tasho Kaletha
Joint IAS/Princeton University Number Theory Seminar Topic: An explicit supercuspidal local Langlands correspondence Speaker: Tasho Kaletha Affiliation: University of Michigan; von Neumann Fellow, School of Mathematics Date: October 29, 2020 For more video please visit http://video.ias.e
From playlist Mathematics

Mazur's program B. - Zureick-Brown - Workshop 2 - CEB T2 2019
David Zureick-Brown (Emory University, Atlanta USA) / 25.06.2019 Mazur's program B. I’ll discuss recent progress on Mazur’s “Program B” – the problem of classifying all possibilities for the “image of Galois” for an elliptic curve over Q (equivalently, classification of all rational poi
From playlist 2019 - T2 - Reinventing rational points

CurvesSurfaces3: De Casteljau Bezier Curves in Algebraic Calculus | N J Wildberger
We explain how to extend Archimedes' famous Parabolic Area Formula to the cubic situation. This formula was historically the first major calculation in Calculus, and gave an explicit and workable formula for the area of a slice of a parabola, cut off by a chord, in terms of the area of a p
From playlist MathSeminars

In this talk, we will define elliptic curves and, more importantly, we will try to motivate why they are central to modern number theory. Elliptic curves are ubiquitous not only in number theory, but also in algebraic geometry, complex analysis, cryptography, physics, and beyond. They were
From playlist An Introduction to the Arithmetic of Elliptic Curves
A new basis theorem for ∑13 sets
Distinguished Visitor Lecture Series A new basis theorem for ∑13 sets W. Hugh Woodin Harvard University, USA and University of California, Berkeley, USA
From playlist Distinguished Visitors Lecture Series
