How to determine if an equation is a linear relation
👉 Learn how to determine if an equation is a linear equation. A linear equation is an equation whose highest exponent on its variable(s) is 1. The variables do not have negative or fractional, or exponents other than one. Variables must not be in the denominator of any rational term and c
From playlist Write Linear Equations

Georges Skandalis - K-théorie à coefficients réels...
K-théorie à coefficients réels et une conjecture de Baum-Connes localisée à l'élément neutre Une difficulté de la conjecture de Baum-Connes, déjà remarquée par Alain Valette, est que, alors que la K-théorie topologique K*top(Γ) d’un groupe – le 'membre de gauche’ de cette conjectu
From playlist Groupes, géométrie et analyse : conférence en l'honneur des 60 ans d'Alain Valette

Classify a polynomial then determining if it is a polynomial or not
👉 Learn how to determine whether a given equation is a polynomial or not. A polynomial function or equation is the sum of one or more terms where each term is either a number, or a number times the independent variable raised to a positive integer exponent. A polynomial equation of functio
From playlist Is it a polynomial or not?

Solve a Bernoulli Differential Equation (Part 2)
This video provides an example of how to solve an Bernoulli Differential Equation. The solution is verified graphically. Library: http://mathispower4u.com
From playlist Bernoulli Differential Equations

👉 Learn about graphing linear equations. A linear equation is an equation whose highest exponent on its variable(s) is 1. i.e. linear equations has no exponents on their variables. The graph of a linear equation is a straight line. To graph a linear equation, we identify two values (x-valu
From playlist ⚡️Graph Linear Equations | Learn About

Determining if a equation is a polynomial or not
👉 Learn how to determine whether a given equation is a polynomial or not. A polynomial function or equation is the sum of one or more terms where each term is either a number, or a number times the independent variable raised to a positive integer exponent. A polynomial equation of functio
From playlist Is it a polynomial or not?

Clément Dell’aiera - Paires de Hecke et K-théorie
Introduites par Shimura en théorie des nombres dans les années 50, les paires de Hecke sont des inclusions de sous-groupes qui sont presque normales : leurs conjugués sont tous commensurables. À une paire de Hecke est associée un groupe localement compact totalement discontinu : sa complét
From playlist Annual meeting “Arbre de Noël du GDR Géométrie non-commutative”

Paolo Piazza: The Novikov conjecture on stratified spaces
A Cheeger space is a smoothly stratified pseudomanifold which is in general non-Witt but that admits an additional structure along the strata that allows for the definition of ideal boundary conditions. An interesting example is given by the reductive Borel-Serre compactification of a Hilb
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

Overview of Linear equations - Free Math Videos - Online Tutor
👉 Learn how to determine if an equation is a linear equation. A linear equation is an equation whose highest exponent on its variable(s) is 1. The variables do not have negative or fractional, or exponents other than one. Variables must not be in the denominator of any rational term and c
From playlist Write Linear Equations

Corinna Ulcigrai - 1/4 Chaotic Properties of Area Preserving Flows
Flows on surfaces are one of the fundamental examples of dynamical systems, studied since Poincaré; area preserving flows arise from many physical and mathematical examples, such as the Novikov model of electrons in a metal, unfolding of billiards in polygons, pseudo-periodic topology. In
From playlist Corinna Ulcigrai - Chaotic Properties of Area Preserving Flows
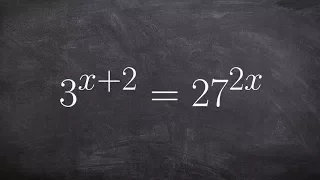
Using one to one property with different bases to solve an exponential equation
👉 Learn how to solve exponential equations. An exponential equation is an equation in which a variable occurs as an exponent. To solve an exponential equation, we isolate the exponential part of the equation. Then we take the log of both sides. Note that the base of the log should correspo
From playlist Solve Exponential Equations without a Calculator

Jintao Deng: The Novikov conjecture and group extensions
Talk by Shintaro Nishikawa in Global Noncommutative Geometry Seminar (Americas) http://www.math.wustl.edu/~xtang/NCG-Seminar.html on August 5, 2020.
From playlist Global Noncommutative Geometry Seminar (Americas)

Quantum cohomology as a deformation of symplectic cohomology - Nicolas Sheridan
IAS/PU-Montreal-Paris-Tel-Aviv Symplectic Geometry Topic: Quantum cohomology as a deformation of symplectic cohomology Speaker: Nicolas Sheridan Affiliation: University of Edinburgh Date: November 13, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

What are the x and y intercepts of a linear equation
👉 Learn about graphing linear equations. A linear equation is an equation whose highest exponent on its variable(s) is 1. i.e. linear equations has no exponents on their variables. The graph of a linear equation is a straight line. To graph a linear equation, we identify two values (x-valu
From playlist ⚡️Graph Linear Equations | Learn About

The Computational Complexity of Geometric Topology Problems - Greg Kuperberg
Greg Kuperberg University of California, Davis September 24, 2012 This talk will be a partial survey of the first questions in the complexity theory of geometric topology problems. What is the complexity, or what are known complexity bounds, for distinguishing n-manifolds for various n? Fo
From playlist Mathematics

Gromov–Witten Invariants and the Virasoro Conjecture. III by Ezra Getzler
J-Holomorphic Curves and Gromov-Witten Invariants DATE:25 December 2017 to 04 January 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore Holomorphic curves are a central object of study in complex algebraic geometry. Such curves are meaningful even when the target has an almost complex stru
From playlist J-Holomorphic Curves and Gromov-Witten Invariants

Determining if equations are linear - Free Math Videos - Online Tutor
👉 Learn how to determine if an equation is a linear equation. A linear equation is an equation whose highest exponent on its variable(s) is 1. The variables do not have negative or fractional, or exponents other than one. Variables must not be in the denominator of any rational term and c
From playlist Write Linear Equations

Shmuel Weinberger - Some introductory remarks on the Novikov conjecture
I will explain a few simple ideas about the Novikov conjecture and related problems Shmuel Weinberger (University of CHICAGO)
From playlist Not Only Scalar Curvature Seminar

Arthur Bartels: The Farrell Jones conjecture for mapping class groups (part 1)
The lecture was held within the framework of the (Junior) Hausdorff Trimester Program Topology: "The Farrell-Jones conjecture" The main step in the proof of the Farrell-Jones conjecture for mapping class groups is the verification of a regularity condition, related to amenability, for the
From playlist HIM Lectures: Junior Trimester Program "Topology"
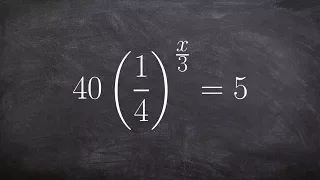
Solve an exponential equation using one to one property and isolating the exponent
👉 Learn how to solve exponential equations. An exponential equation is an equation in which a variable occurs as an exponent. To solve an exponential equation, we isolate the exponential part of the equation. Then we take the log of both sides. Note that the base of the log should correspo
From playlist Solve Exponential Equations with Logarithms