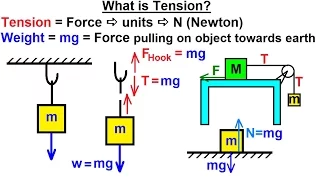
Physics - Mechanics: Ch 17 Tension and Weight (1 of 11) What is Tension?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is tension and how to calculate tension using the free-body diagram. Next video in this series can be seen at: https://youtu.be/BxUhaktD8PA
From playlist PHYSICS MECHANICS 1: INTRO, VECTORS, MOTION, PROJECTILE MOTION, NEWTON'S LAWS

Louis Theran: Rigidity of Random Graphs in Higher Dimensions
I will discuss rigidity properties of binomial random graphs G(n,p(n)) in fixed dimension d and some related problems in low-rank matrix completion. The threshold for rigidity is p(n) = Θ(log n / n), which is within a multiplicative constant of optimal. This talk is based on joint work wi
From playlist HIM Lectures 2015

Rigidity phenomena in random point sets and applications - Subhroshekhar Ghosh
Subhroshekhar Ghosh Princeton University December 11, 2013 In several naturally occurring (infinite) point processes, we show that the number (and other statistical properties) of the points inside a finite domain are determined, almost surely, by the point configuration outside the domain
From playlist Mathematics

Andrey Gogolev: Rigidity in rank one: dynamics and geometry - lecture 2
A dynamical system is called rigid if a weak form of equivalence with a nearby system, such as coincidence of some simple invariants, implies a strong form of equivalence. In this minicourse we will discuss smooth rigidity of hyperbolic dynamical systems and related geometric questions suc
From playlist Dynamical Systems and Ordinary Differential Equations

Andrey Gogolev: Rigidity in rank one: dynamics and geometry - lecture 3
A dynamical system is called rigid if a weak form of equivalence with a nearby system, such as coincidence of some simple invariants, implies a strong form of equivalence. In this minicourse we will discuss smooth rigidity of hyperbolic dynamical systems and related geometric questions suc
From playlist Dynamical Systems and Ordinary Differential Equations

Andrey Gogolev: Rigidity in rank one: dynamics and geometry - lecture 1
A dynamical system is called rigid if a weak form of equivalence with a nearby system, such as coincidence of some simple invariants, implies a strong form of equivalence. In this minicourse we will discuss smooth rigidity of hyperbolic dynamical systems and related geometric questions suc
From playlist Dynamical Systems and Ordinary Differential Equations

Center of Mass & Center of Rigidity | Reinforced Concrete Design
http://goo.gl/nmipcn for more FREE video tutorials covering Concrete Structural Design The objectives of this video are to briefly discuss about the center of mass and center of rigidity by understanding what their means as well as to talks about combination of center of mass and center o
From playlist SpoonFeedMe: Concrete Structures

Symmetry in Physics | Noether's theorem
▶ Topics ◀ Global / Local Symmetries, Continuous / Discrete Symmetries ▶ Social Media ◀ [Instagram] @prettymuchvideo ▶ Music ◀ TheFatRat - Fly Away feat. Anjulie https://open.spotify.com/track/1DfFHyrenAJbqsLcpRiOD9 If you want to help us get rid of ads on YouTube, you can support us on
From playlist Symmetry

Dimensions (1 of 3: The Traditional Definition - Directions)
More resources available at www.misterwootube.com
From playlist Exploring Mathematics: Fractals

MIT RES.TLL-004 Concept Vignettes View the complete course: http://ocw.mit.edu/RES-TLL-004F13 Instructor: Dan Frey This video uses robotics as a context for describing rigid body motion and equations of constraint. Illustrative video clips are drawn from the robotics competition in MIT's
From playlist MIT STEM Concept Videos

Introduction to transformations | Transformations | Geometry | Khan Academy
Introduction to transformations Practice this lesson yourself on KhanAcademy.org right now: https://www.khanacademy.org/math/geometry/transformations/rigid-transformations-intro/e/performing-translations-on-the-coordinate-plane?utm_source=YT&utm_medium=Desc&utm_campaign=Geometry Watch t
From playlist High School Geometry | High School Math | Khan Academy

Teaching Rigid Body Dynamics, Part 1: Computational Thinking
This introduction to the computational thinking approach explores basic concepts and discusses how the approach can support the teaching of rigid body dynamics. Get a free product Trial: https://goo.gl/ZHFb5u Learn more about MATLAB: https://goo.gl/8QV7ZZ Learn more about Simulink: https:
From playlist Teaching Rigid Body Dynamics

MIT RES.TLL-004 Concept Vignettes View the complete course: http://ocw.mit.edu/RES-TLL-004F13 Instructor: Dan Frey This video leads students through describing the motion of all points on a wobbly disk as a function of time. Properties of time independent rotation matrices are explored.
From playlist MIT STEM Concept Videos

IMS Public Lecture: Order and Rigidity Sensing by Biological Cells
Samuel Safran, Weizmann Institute of Science, Israel
From playlist Public Lectures

Mylène Maïda: A statistical physics approach to the sine beta process
The universality properties of the Sine process (corresponding to inverse temperature beta equal to 2) are now well known. More generally, a family of point processes have been introduced by Valko and Virag and shown to be the bulk limit of Gaussian beta ensembles, for any positive beta. T
From playlist Probability and Statistics

First order rigidity of high-rank arithmetic groups - Alexander Lubotzky
Arithmetic Groups Topic: First order rigidity of high-rank arithmetic groups Speaker: Alexander Lubotzky Affiliation: Hebrew University of Jerusalem; Visiting Professor, School of Mathematics Date: October 6, 2021 The family of high-rank arithmetic groups is a class of groups playing an
From playlist Mathematics

Erica Flapan (9/18/18): Topological and geometric symmetries of molecular structures
How does a chemist know that a molecule that he or she has synthesized has the desired form? Most non-biological molecules are too small to see in a microscope or even with the help of an electron micrograph. So chemists need to collect experimental data as evidence that a synthetic mole
From playlist AATRN 2018

Washington Taylor - How Natural is the Standard Model in the String Landscape?
Mike's pioneering work in taking a statistical approach to string vacua has contributed to an ever-improving picture of the landscape of solutions of string theory. In this talk, we explore how such statistical ideas may be relevant in understanding how natural different realizations of th
From playlist Mikefest: A conference in honor of Michael Douglas' 60th birthday

Bill Jackson: Generic Rigidity of Point Line Frameworks
A point-line framework is a collection of points and lines in the plane which are linked by pairwise constraints that fix some angles between pairs of lines and also some point-line and point-point distances. It is rigid if every continuous motion of the points and lines which preserves th
From playlist HIM Lectures 2015

Fabrizio Catanese: New examples of rigid varieties and criteria for fibred surfaces [...]
Abstract: Given an algebraic variety defined by a set of equations, an upper bound for its dimension at one point is given by the dimension of the Zariski tangent space. The infinitesimal deformations of a variety X play a somehow similar role, they yield the Zariski tangent space at the
From playlist Algebraic and Complex Geometry