
Vector Calculus 1: What Is a Vector?
https://bit.ly/PavelPatreon https://lem.ma/LA - Linear Algebra on Lemma http://bit.ly/ITCYTNew - Dr. Grinfeld's Tensor Calculus textbook https://lem.ma/prep - Complete SAT Math Prep
From playlist Vector Calculus

Multivariable Calculus | The notion of a vector and its length.
We define the notion of a vector as it relates to multivariable calculus and define its length. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Vectors for Multivariable Calculus

Vectors | Lecture 1 | Vector Calculus for Engineers
Defines vectors, vector addition and vector subtraction. Join me on Coursera: https://www.coursera.org/learn/vector-calculus-engineers Lecture notes at http://www.math.ust.hk/~machas/vector-calculus-for-engineers.pdf Subscribe to my channel: http://www.youtube.com/user/jchasnov?sub_con
From playlist Vector Calculus for Engineers
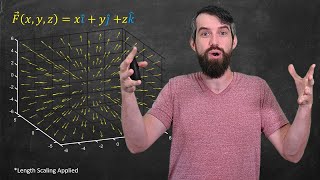
Intro to VECTOR FIELDS // Sketching by hand & with computers
Vector Fields are extremely important in math, physics, engineering, and many other fields. Gravitational fields, electric fields, magnetic fields, velocity fields, these are all examples of vector fields. In this video we will define the concept of a vector field, talk about some basic te

Scalar and vector fields | Lecture 11 | Vector Calculus for Engineers
Definition of a scalar and vector field. How to visualize a two-dimensional vector field. Join me on Coursera: https://www.coursera.org/learn/vector-calculus-engineers Lecture notes at http://www.math.ust.hk/~machas/vector-calculus-for-engineers.pdf Subscribe to my channel: http://www
From playlist Vector Calculus for Engineers

Linear Algebra for Computer Scientists. 1. Introducing Vectors
This computer science video is one of a series on linear algebra for computer scientists. This video introduces the concept of a vector. A vector is essentially a list of numbers that can be represented with an array or a function. Vectors are used for data analysis in a wide range of f
From playlist Linear Algebra for Computer Scientists

A short refresher on vectors. Before I introduce vector-based functions, it's important to look at vectors themselves and how they are represented in python™ and the IPython Notebook using SymPy.
From playlist Life Science Math: Vectors

Calculus 3: Vector Calculus in 2D (8 of 39) Adding Vectors (Components are Known)
Visit http://ilectureonline.com for more math and science lectures! In this video I will find the resultant vector given the components of vectors A and B are known. Next video in the series can be seen at: https://youtu.be/e1-OvKiLsho
From playlist CALCULUS 3 CH 3 VECTOR CALCULUS

Vector Calculus 5: Vector Equation of a Straight Line
https://bit.ly/PavelPatreon https://lem.ma/LA - Linear Algebra on Lemma http://bit.ly/ITCYTNew - Dr. Grinfeld's Tensor Calculus textbook https://lem.ma/prep - Complete SAT Math Prep
From playlist Vector Calculus
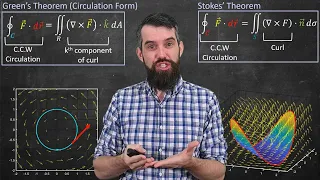
A unified view of Vector Calculus (Stoke's Theorem, Divergence Theorem & Green's Theorem)
In the final video of my vector calculus playlist (congrats to everyone for making it to the end!!!) I want to do a bit of an overview of the major theorems we have seen in this course - Stokes' Theorem, Divergence Theorem, Green's Theorem - all are part of a unified framework. Loosely, in

Promotional Video | Vector Calculus for Engineers
My promotional video for my free-to-audit Coursera course, Vector Calculus for Engineers. Why should engineers learn vector calculus? Join me on Coursera: https://www.coursera.org/learn/vector-calculus-engineers Lecture notes at http://www.math.ust.hk/~machas/vector-calculus-for-engin
From playlist Vector Calculus for Engineers

A random lecture from Calculus III
A random lecture from my Calculus III class from fall 2020. It follows Volume 4 of Calculus Illustrated by Peter Saveliev. See http://calculus123.com.
From playlist Calculus III

Vector Calculus and Partial Differential Equations: Big Picture Overview
This video describes how vector calculus is the language we use to derive partial differential equations (PDEs) to encode physical laws, such as mass, momentum, and energy conservation in fluids. This is the first lecture of a series that will describe Div, Grad, and Curl; Gauss and Stoke
From playlist Engineering Math: Vector Calculus and Partial Differential Equations

Find a Unit Vector in the Direction of a Given Vector with Length 4.
In this video we are given a vector and we are asked to find another vector in the same direction but with length 4. I hope this helps someone who is studying calculus and learning about vectors. Great Calculus Book: https://amzn.to/3VfotAU This is my affiliate link. As an Amazon Associa
From playlist Vectors

The Ultimate Multivariable Calculus Workbook
In this video I will show you this amazing workbook which you can use to learn multivariable calculus. This workbook has tons of problems and includes full solutions to every single problem. Some of the topics covered include Partial Differentiation, The Chain Rule, Vector Calculus, Line I
From playlist Book Reviews

INTRODUCTION to VECTOR CALCULUS calculus 3
This video is the first in a series of videos which serve as an introduction to vector calculus and calculus 3. These videos are intended as supplemental material for the course MATH2021 which I am presently teaching at the University of Sydney. 0:00 Introduction and chit chat 2:48 Main
From playlist All Videos

Find a Unit Vector in the Direction of Another Vector
In this video we find a unit vector in the direction of another vector. I hope this helps someone who is studying calculus and learning about vectors. Great Calculus Book: https://amzn.to/3VfotAU This is my affiliate link. As an Amazon Associate I earn from qualifying purchases. If you en
From playlist Vectors

Vector Calculus 23: The Laws of Vector Differentiation
https://bit.ly/PavelPatreon https://lem.ma/LA - Linear Algebra on Lemma http://bit.ly/ITCYTNew - Dr. Grinfeld's Tensor Calculus textbook https://lem.ma/prep - Complete SAT Math Prep
From playlist Vector Calculus
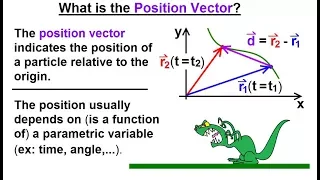
Calculus 3: Vector Calculus in 2D (17 of 39) What is the Position Vector?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is the position vector. The position vector indicates the position of a particle relative to the origin. The position usually depends on, or is a function of, a parametric variable (ex. t
From playlist CALCULUS 3 CH 3 VECTOR CALCULUS
