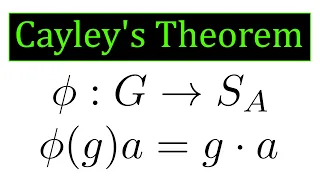Finite groups | Permutation groups
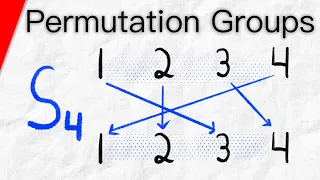
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M and whose group operation is the composition of permutations in G (which are thought of as bijective functions from the set M to itself). The group of all permutations of a set M is the symmetric group of M, often written as Sym(M). The term permutation group thus means a subgroup of the symmetric group. If M = {1, 2, ..., n} then Sym(M) is usually denoted by Sn, and may be called the symmetric group on n letters. By Cayley's theorem, every group is isomorphic to some permutation group. The way in which the elements of a permutation group permute the elements of the set is called its group action. Group actions have applications in the study of symmetries, combinatorics and many other branches of mathematics, physics and chemistry. (Wikipedia).