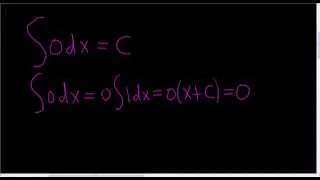
The Constant of Integration is ALWAYS Zero
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys The Constant of Integration is ALWAYS Zero
From playlist Math Magic

I define one of the most important constants in mathematics, the Euler-Mascheroni constant. It intuitively measures how far off the harmonic series 1 + 1/2 + ... + 1/n is from ln(n). In this video, I show that the constant must exist. It is an open problem to figure out if the constant is
From playlist Series

How an Equilibrium Constant varies with Temperature - Thermodynamics - Physical Chemistry
Deriving a quantitative relationship to show how an equilibrium constant varies with temperature and so showing were Le Chatelier's Principle comes from in this context. Along the way, the Gibbs-Helmholtz van't Hoff equations are derived and used. My video for deriving the thermodynamics
From playlist Introductory Thermodynamics

The limit is the limit is the limit is the limit
Here I evaluate a neat infinite limit with l'Hopital's rule... does it work though? Subscribe to my channel: https://youtube.com/drpeyam Check out my TikTok channel: https://www.tiktok.com/@drpeyam Follow me on Instagram: https://www.instagram.com/peyamstagram/ Follow me on Twitter: https
From playlist Calculus

In this video, I show a really neat result, namely that the maximum of two continuous functions is continuous. Enjoy the epsilon-delta extravaganza! Continuity Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmB86yhDeAUZPY0dktFtb8Tj Subscribe to my channel: https://youtube.com/d
From playlist Limits and Continuity

Matt Parker talks about numbers - as he often does. His book "Humble Pi" is at: http://bit.ly/Humble_Pi More links & stuff in full description below ↓↓↓ The book on Amazon: https://amzn.to/2NKposg Numberphile podcast is on your podcast player. Or the website is: https://www.numberphile.c
From playlist Matt Parker (standupmaths) on Numberphile

This statement is false. Think about it, and it makes your head hurt. If it’s true, it’s false. If it’s false, it’s true. In 1931, Austrian logician Kurt Gödel shocked the worlds of mathematics and philosophy by establishing that such statements are far more than a quirky turn of language:
From playlist Explore the World Science Festival

Gregory Chaitin - How is Mathematics Truth and Beauty?
When mathematicians speak about their craft, why do they use terms of philosophy and art? What is it about mathematics that can penetrate trivial truth and reveal fundamental “Truth?” What are the characteristics of fundamental truth? What is it about mathematics that can elicit the descri
From playlist How is Mathematics Truth and Beauty? - CTT Interview Series

Gregory Chaitin - Is Mathematics Invented or Discovered?
Free access to Closer to Truth's library of 5,000 videos: http://bit.ly/376lkKN Mathematics describes the real world of atoms and acorns, stars and stairs, with remarkable precision. So is mathematics invented by humans just like chisels and hammers and pieces of music? Or is mathematics
From playlist Is Mathematics Invented or Discovered? - CTT Interview Series

Kolmogorov Complexity - Applied Cryptography
This video is part of an online course, Applied Cryptography. Check out the course here: https://www.udacity.com/course/cs387.
From playlist Applied Cryptography

Identifying constant of proportionality graphically
Identifying constant of proportionality graphically
From playlist Algebra 1 | Get Ready for Grade Level | Khan Academy

Gregory Chaitin - What Can Science Say About God?
Most scientists believe that science can say nothing about God other than to show that there is no need for such a being. Scientists claim that science is quite capable of providing most explanations today and virtually all explanations in the future. Click here to watch more interviews
From playlist Big Questions About God - Closer To Truth - Core Topic

Can Science Talk God? | Episode 711 | Closer To Truth
Some say that science and God are not related. Others, that science describes a world that evidences "God's handiwork," or a world that works just fine without God. Featuring interviews with David Gross, William Dembski, Victor Stenger, Gregory Chaitin, and George Smoot. Season 7, Episode
From playlist Big Questions About God - Closer To Truth - Core Topic

Is Mathematics Invented or Discovered? | Episode 409 | Closer To Truth
Mathematics describes the real world of atoms and acorns, stars and stairs, with remarkable precision. So is mathematics invented by humans-like chisels and hammers and pieces of music? Or is mathematics discovered-always out there, somewhere, like mysterious islands waiting to be found? F
From playlist Closer To Truth | Season 4

Epsilon Delta Continuity (Example 6): 1/x
In this video, I use the epsilon-delta definition of continuity to show that f(x) = 1/x is continuous. This is a must-see for every calculus lover, enjoy! Continuity Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmB86yhDeAUZPY0dktFtb8Tj Subscribe to my channel: https://youtube
From playlist Limits and Continuity
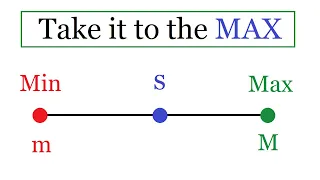
Maximum and Minimum of a set In this video, I define the maximum and minimum of a set, and show that they don't always exist. Enjoy! Check out my Real Numbers Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmCZggpJZvUXnUzaw7fHCtoh
From playlist Real Numbers

Maximum modulus principle In this video, I talk about the maximum modulus principle, which says that the maximum of the modulus of a complex function is attained on the boundary. I also show that the same thing is true for the real and imaginary parts, and finally I discuss the strong max
From playlist Complex Analysis
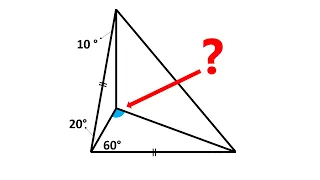
Looks Easy But Is Insanely Hard
Many people asked me to solve this one! What is the value of x? Many more solutions https://twitter.com/preshtalwalkar/status/1254337151359234049 Solution by Ahmet ÇETİN https://twitter.com/ahmetcet_n/status/1254557842733924354 Subscribe: https://www.youtube.com/user/MindYourDecisions?s
From playlist Math Puzzles, Riddles And Brain Teasers

There's more over on Veritasium! "What is NOT Random?": https://www.youtube.com/watch?v=sMb00lz-IfE SOURCES AND MORE BELOW! My twitter: https://twitter.com/tweetsauce My instagram: http://instagram.com/electricpants Generate random numbers using atmospheric noise: http://www.random.org/
From playlist Knowledge

Here I show that the ratio of two continuous functions is continuous. I do it both by using epsilon-delta and the sequence definition of continuity. Interestingly, the proof is similar to the proof of the quotient rule for derivatives. Enjoy! Reciprocals of limits: https://youtu.be/eRs84C
From playlist Limits and Continuity