
We show the connection between the method of adjoints in optimal control to the implicit function theorem ansatz. We relate the costate or adjoint state variable to Lagrange multipliers.
From playlist There and Back Again: A Tale of Slopes and Expectations (NeurIPS-2020 Tutorial)
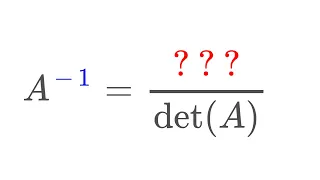
In this video, I define the notion of adjugate matrix and use it to calculate A-1 using determinants. This is again beautiful in theory, but inefficient in examples. Adjugate matrix example: https://youtu.be/OFykHi0idnQ Check out my Determinants Playlist: https://www.youtube.com/playlist
From playlist Determinants

Adjoint Equation of a Linear System of Equations - by implicit derivative
Automatic Differentiation allows for easily propagating derivatives through explicit relations. The adjoint method also enables efficient derivatives over implicit relations like linear systems, which enables the computation of sensitivities. Here are the notes: https://raw.githubuserconte
From playlist Summer of Math Exposition Youtube Videos

Algebraic properties of the adjoint. Null space and range of the adjoint. The matrix of T* is the conjugate transpose of the matrix of T.
From playlist Linear Algebra Done Right

Ex: Integration by Parts Involving a Trig and Linear Function (x*cos(4x))
This video provides an example of integration by parts. The integrand is a product of a linear function and a trigonometric function. Site: http://mathispower4u.com
From playlist Integration by Parts

Adjoint / Daggered Operators in Quantum Mechanics
In this video, we will explain adjoint operators in quantum mechanics. First of all, for any operator A, we can define its adjoint, A-dagger, via this equation. The idea behind this is, that while operators in quantum mechanics usually act towards the right, adjoint operators act to the le
From playlist Quantum Mechanics, Quantum Field Theory

Matrices | Adjoint of a Matrix (Examples) | Don't Memorise
What is the Adjoint of a Matrix? ✅To learn more about, Matrices, enroll in our full course now: https://infinitylearn.com/microcourses?utm_source=youtube&utm_medium=Soical&utm_campaign=DM&utm_content=hiuqyvR-f_4&utm_term=%7Bkeyword%7D In this video, we will learn: 0:00 how to find adjo
From playlist Matrices

The Inverse of a 2 by 2 Matrix Using the Adjoint Method
This video explains how to find the inverse matrix of a 2 by 2 matrix using the adjoint method.
From playlist Inverse Matrices

Integration by Parts (After Integration by Parts Basics)
These examples are a little more involved then the Integration by Part - The Basics http://mathispower4u.wordpress.com/
From playlist Integration Intro

Optimal control problem for Burgers’ equation - Mythily Ramaswamy
PROGRAM: Data Assimilation Research Program Venue: Centre for Applicable Mathematics-TIFR and Indian Institute of Science Dates: 04 - 23 July, 2011 DESCRIPTION: Data assimilation (DA) is a powerful and versatile method for combining observational data of a system with its dynamical mod
From playlist Data Assimilation Research Program

Data-Driven Control: Balanced Proper Orthogonal Decomposition
In this lecture, we introduce the balancing proper orthogonal decomposition (BPOD) to approximate balanced truncation for high-dimensional systems. https://www.eigensteve.com/
From playlist Data-Driven Control with Machine Learning

Stefan Volkwein: Introduction to PDE-constrained optimization - lecture 2
HYBRID EVENT Recorded during the meeting "Domain Decomposition for Optimal Control Problems" the September 06, 2022 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematici
From playlist Jean-Morlet Chair - Gander/Hubert

Lars Ruthotto: "Deep Neural Networks Motivated By Differential Equations (Part 1/2)"
Watch part 2/2 here: https://youtu.be/1mVycBKb1TE Machine Learning for Physics and the Physics of Learning Tutorials 2019 "Deep Neural Networks Motivated By Differential Equations (Part 1/2)" Lars Ruthotto, Emory University Abstract: In this short course, we establish the connection bet
From playlist Machine Learning for Physics and the Physics of Learning 2019

PROGRAM: Data Assimilation Research Program Venue: Centre for Applicable Mathematics-TIFR and Indian Institute of Science Dates: 04 - 23 July, 2011 DESCRIPTION: Data assimilation (DA) is a powerful and versatile method for combining observational data of a system with its dynamical mod
From playlist Data Assimilation Research Program

Andy Wathen: Parallel preconditioning for time-dependent PDEs and PDE control
We present a novel approach to the solution of time-dependent PDEs via the so-called monolithic or all-at-once formulation. This approach will be explained for simple parabolic problems and its utility in the context of PDE constrained optimization problems will be elucidated. The underlyi
From playlist Numerical Analysis and Scientific Computing

Optional structures for transient growth by Ritabrata Thakur
DISCUSSION MEETING FLUIDS DAY ORGANIZERS: Rama Govindarajan, Samriddhi Sankar Ray and Gaurav Tomar DATE : 20 January 2020 VENUE: Ramanujan Lecture Hall, ICTS Bangalore The fluid mechanics community in Bangalore has expanded enormously with different physics and engineering departments
From playlist Fluids Day 2020

Apportionment: Hamilton's Method
This video explains and provides an example of the Hamilton's method of apportionment.. Site: http://mathispower4u.com
From playlist Apportionment

