
We show the connection between the method of adjoints in optimal control to the implicit function theorem ansatz. We relate the costate or adjoint state variable to Lagrange multipliers.
From playlist There and Back Again: A Tale of Slopes and Expectations (NeurIPS-2020 Tutorial)

Adjoint / Daggered Operators in Quantum Mechanics
In this video, we will explain adjoint operators in quantum mechanics. First of all, for any operator A, we can define its adjoint, A-dagger, via this equation. The idea behind this is, that while operators in quantum mechanics usually act towards the right, adjoint operators act to the le
From playlist Quantum Mechanics, Quantum Field Theory

Algebraic properties of the adjoint. Null space and range of the adjoint. The matrix of T* is the conjugate transpose of the matrix of T.
From playlist Linear Algebra Done Right
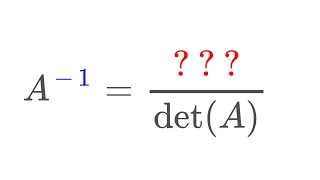
In this video, I define the notion of adjugate matrix and use it to calculate A-1 using determinants. This is again beautiful in theory, but inefficient in examples. Adjugate matrix example: https://youtu.be/OFykHi0idnQ Check out my Determinants Playlist: https://www.youtube.com/playlist
From playlist Determinants

The Inverse of a 2 by 2 Matrix Using the Adjoint Method
This video explains how to find the inverse matrix of a 2 by 2 matrix using the adjoint method.
From playlist Inverse Matrices

Self-adjoint operators. All eigenvalues of a self-adjoint operator are real. On a complex vector space, if the inner product of Tv and v is real for every vector v, then T is self-adjoint.
From playlist Linear Algebra Done Right

Matrices | Adjoint of a Matrix (Examples) | Don't Memorise
What is the Adjoint of a Matrix? ✅To learn more about, Matrices, enroll in our full course now: https://infinitylearn.com/microcourses?utm_source=youtube&utm_medium=Soical&utm_campaign=DM&utm_content=hiuqyvR-f_4&utm_term=%7Bkeyword%7D In this video, we will learn: 0:00 how to find adjo
From playlist Matrices

Find the Cofactor Matrix and Adjoint Matrix (2 by 2)
This video explains how to find the cofactor matrix and adjoint matrix for a 2 by 2 matrix.
From playlist The Determinant of a Matrix

Inverse of 4x4 Matrix Using Adjugate Formula
Typo around 4:15. In the cofactor grid, the matrix in the first column, third row, C(3,1) should have bottom row (0, 1, 4), not (2, 1, 4). This is a typo, as the following work uses the correct numbers. (Thanks to Amin Haddad!) Linear Algebra: We find the inverse of a 4x4 matrix usin
From playlist MathDoctorBob: Linear Algebra I: From Linear Equations to Eigenspaces | CosmoLearning.org Mathematics

Adjoint Equation of a Linear System of Equations - by implicit derivative
Automatic Differentiation allows for easily propagating derivatives through explicit relations. The adjoint method also enables efficient derivatives over implicit relations like linear systems, which enables the computation of sensitivities. Here are the notes: https://raw.githubuserconte
From playlist Summer of Math Exposition Youtube Videos

Toshiaki Hishida : Lq-Lr estimates of a generalized Oseen evolution operator...
Abstract: Consider the motion of a viscous incompressible fluid in a 3D exterior domain D when a rigid body ℝ3∖D moves with prescribed time-dependent translational and angular velocities. For the linearized non-autonomous system, Lq-Lr smoothing action near t=s as well as generation of the
From playlist Mathematical Physics

Normal operators. Characterization of normal operators by ||Tv|| = ||T*v|| for all v. Eigenvectors of a normal operator corresponding to distinct eigenvalues are orthogonal.
From playlist Linear Algebra Done Right
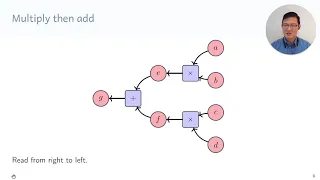
Investigate the forward backward algorithm of hidden Markov models, by deriving the backward algorithm using reverse mode automatic differentiation.
From playlist There and Back Again: A Tale of Slopes and Expectations (NeurIPS-2020 Tutorial)

Data-Driven Control: Balanced Proper Orthogonal Decomposition
In this lecture, we introduce the balancing proper orthogonal decomposition (BPOD) to approximate balanced truncation for high-dimensional systems. https://www.eigensteve.com/
From playlist Data-Driven Control with Machine Learning

The Inverse of a 4 by 4 Matrix Given the Determinant and Cofactor Matrix
This video explains how to find the inverse matrix of a 4 by 4 matrix using the adjoint method given the determinant and the cofactor matrix.
From playlist Inverse Matrices

