
These sculptures are joint work with Roice Nelson. They are available from shapeways.com at http://shpws.me/oNgi, http://shpws.me/oqOx and http://shpws.me/orB8.
From playlist 3D printing
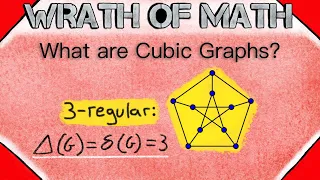
What are Cubic Graphs? | Graph Theory
What are cubic graphs? We go over this bit of graph theory in today's math lesson! Recall that a regular graph is a graph in which all vertices have the same degree. The degree of a vertex v is the number of edges incident to v, or equivalently the number of vertices adjacent to v. If ever
From playlist Graph Theory

Reaching for Infinity Through Honeycombs – Roice Nelson
Pick any three integers larger than 2. We describe how to understand and draw a picture of a corresponding kaleidoscopic {p,q,r} honeycomb, up to and including {∞,∞,∞}.
From playlist G4G12 Videos

A number pattern that results in numbers with 8 for a digit
From playlist Number Patterns

A fun number pattern built from the number 987654321
From playlist Number Patterns

Sudoku Colorings of a 16-cell Pre-Fractal – Hideki Tsuiki
This is a joint work with Yasuyuki Tsukamoto. 16-cell is a 4-dimensional polytope with a lot of beautiful properties, in particular with respect to cubic projections of a fractal based on it. We define SUDOKU-like colorings of a 3D cubic lattice which is defined based on properties of a
From playlist G4G12 Videos

7. Natural Honeycombs: Cork; Foams: Linear Elasticity
MIT 3.054 Cellular Solids: Structure, Properties and Applications, Spring 2015 View the complete course: http://ocw.mit.edu/3-054S15 Instructor: Lorna Gibson This session begins with a look at cork as a natural honeycomb structure, and covers properties of foams and some modeling. Licens
From playlist MIT 3.054 Cellular Solids: Structure, Properties and Applications, Spring 2015

Cubic and Reciprocal Graphs: Find Cubic Equation From Sketch (2 Solutions) (Grade 9) - Maths
Topic: Cubic and Reciprocal Graphs: Find Cubic Equation From Sketch (2 Solutions) Do this paper online for free: https://www.onmaths.com/cubic-and-reciprocal-graphs/ Grade: 9 This question appears on calculator and non-calculator higher GCSE papers. Practise and revise with OnMaths. Go to
From playlist Cubic and Reciprocal Graphs

MIT 3.054 Cellular Solids: Structure, Properties and Applications, Spring 2015 View the complete course: http://ocw.mit.edu/3-054S15 Instructor: Lorna Gibson This session covers wood structure, micro-structure, stress-strain, honeycomb models, and bending. License: Creative Commons BY-NC
From playlist MIT 3.054 Cellular Solids: Structure, Properties and Applications, Spring 2015

Canonical structures inside the Platonic solids III | Universal Hyperbolic Geometry 51
The dodecahedron is surely one of the truly great mathematical objects---revered by the ancient Greeks, Kepler, and many mathematicians since. Its symmetries are particularly rich, and in this video we look at how to see the five-fold and six-fold symmetries of this object via internal str
From playlist Universal Hyperbolic Geometry

Inverse problem by Abhinav Kumar
DISCUSSION MEETING SPHERE PACKING ORGANIZERS: Mahesh Kakde and E.K. Narayanan DATE: 31 October 2019 to 06 November 2019 VENUE: Madhava Lecture Hall, ICTS Bangalore Sphere packing is a centuries-old problem in geometry, with many connections to other branches of mathematics (number the
From playlist Sphere Packing - 2019

Bitangents to plane quartics - tropical, real and arithmetic count by Hannah Markwig
PROGRAM COMBINATORIAL ALGEBRAIC GEOMETRY: TROPICAL AND REAL (HYBRID) ORGANIZERS Arvind Ayyer (IISc, India), Madhusudan Manjunath (IITB, India) and Pranav Pandit (ICTS-TIFR, India) DATE: 27 June 2022 to 08 July 2022 VENUE: Madhava Lecture Hall and Online Algebraic geometry is the study of
From playlist Combinatorial Algebraic Geometry: Tropical and Real (HYBRID)

3 - Kick-off afternoon : Thomas Hales, Formalizing the proof of the Kepler Conjecture
Thomas Hales (University of Pittsburgh): Formalizing the proof of the Kepler Conjecture
From playlist T2-2014 : Semantics of proofs and certified mathematics

An Introduction to Tensor Renormalization Group (Lecture 4) by Daisuke Kadoh
PROGRAM NONPERTURBATIVE AND NUMERICAL APPROACHES TO QUANTUM GRAVITY, STRING THEORY AND HOLOGRAPHY (HYBRID) ORGANIZERS: David Berenstein (University of California, Santa Barbara, USA), Simon Catterall (Syracuse University, USA), Masanori Hanada (University of Surrey, UK), Anosh Joseph (II
From playlist NUMSTRING 2022

Supersymmetry on the lattice: Geometry, Topology, and Spin Liquids by Simon Trebst
PROGRAM FRUSTRATED METALS AND INSULATORS (HYBRID) ORGANIZERS Federico Becca (University of Trieste, Italy), Subhro Bhattacharjee (ICTS-TIFR, India), Yasir Iqbal (IIT Madras, India), Bella Lake (Helmholtz-Zentrum Berlin für Materialien und Energie, Germany), Yogesh Singh (IISER Mohali, In
From playlist FRUSTRATED METALS AND INSULATORS (HYBRID, 2022)

Particle distribution in a honeycomb maze with rounded cells
This simulation shows the particle distribution in a honeycomb maze, which was introduced in the video https://youtu.be/a3ICP1wQyR8 . The walls of each hexagonal cell are part of a same circle which is inscribed in the hexagon. As we have seen in the previous video, particles can spend lon
From playlist Illumination problem

The Mysterious Architecture of the Universe - with J Richard Gott
J Richard Gott leads a journey through the history of our understanding of the Universe’s structure, and explains the ‘cosmic web’: the idea that our Universe is like a sponge made up of clusters of galaxies intricately connected by filaments of galaxies. Watch the Q&A here: https://youtu
From playlist Ri Talks

8. Foams: Non-linear Elasticity
MIT 3.054 Cellular Solids: Structure, Properties and Applications, Spring 2015 View the complete course: http://ocw.mit.edu/3-054S15 Instructor: Lorna Gibson This session begins with a viewing of video on Hooke's Micrographia, then covers compressive strength and fracture toughness of foa
From playlist MIT 3.054 Cellular Solids: Structure, Properties and Applications, Spring 2015

Monomer Percolation by Kedar Damle
PROGRAM FRUSTRATED METALS AND INSULATORS (HYBRID) ORGANIZERS Federico Becca (University of Trieste, Italy), Subhro Bhattacharjee (ICTS-TIFR, India), Yasir Iqbal (IIT Madras, India), Bella Lake (Helmholtz-Zentrum Berlin für Materialien und Energie, Germany), Yogesh Singh (IISER Mohali, In
From playlist FRUSTRATED METALS AND INSULATORS (HYBRID, 2022)

Cubic and Reciprocal Graphs: Draw Graph Of A Circle (Grade 6) - OnMaths GCSE Maths Revision
Topic: Cubic and Reciprocal Graphs: Draw Graph Of A Circle Do this paper online for free: https://www.onmaths.com/cubic-and-reciprocal-graphs/ Grade: 6 This question appears on calculator higher GCSE papers. Practise and revise with OnMaths. Go to onmaths.com for more resources, like pred
From playlist Cubic and Reciprocal Graphs