Vertical and horizontal bundles

Fiber bundles | Differential topology | Connection (mathematics)

In mathematics, the vertical bundle and the horizontal bundle are vector bundles associated to a smooth fiber bundle. More precisely, given a smooth fiber bundle , the vertical bundle and horizontal bundle are subbundles of the tangent bundle of whose Whitney sum satisfies . This means that, over each point , the fibers and form complementary subspaces of the tangent space . The vertical bundle consists of all vectors that are tangent to the fibers, while the horizontal bundle requires some choice of complementary subbundle. To make this precise, define the vertical space at to be . That is, the differential (where ) is a linear surjection whose kernel has the same dimension as the fibers of . If we write , then consists of exactly the vectors in which are also tangent to . The name is motivated by low-dimensional examples like the trivial line bundle over a circle, which is sometimes depicted as a vertical cylinder projecting to a horizontal circle. A subspace of is called a horizontal space if is the direct sum of and . The disjoint union of the vertical spaces VeE for each e in E is the subbundle VE of TE; this is the vertical bundle of E. Likewise, provided the horizontal spaces vary smoothly with e, their disjoint union is a horizontal bundle. The use of the words "the" and "a" here is intentional: each vertical subspace is unique, defined explicitly by . Excluding trivial cases, there are an infinite number of horizontal subspaces at each point. Also note that arbitrary choices of horizontal space at each point will not, in general, form a smooth vector bundle; they must also vary in an appropriately smooth way. The horizontal bundle is one way to formulate the notion of an Ehresmann connection on a fiber bundle. Thus, for example, if E is a principal G-bundle, then the horizontal bundle is usually required to be G-invariant: such a choice is equivalent to a connection on the principal bundle. This notably occurs when E is the frame bundle associated to some vector bundle, which is a principal bundle. (Wikipedia).

Horizontal and Vertical Lines

Some of the links below are affiliate links. As an Amazon Associate I earn from qualifying purchases. If you purchase through these links, it won't cost you any additional cash, but it will help to support my channel. Thank you! ►PRODUCT RECOMMENDATIONS https://www.amazon.com/shop/brithem

From playlist Algebra

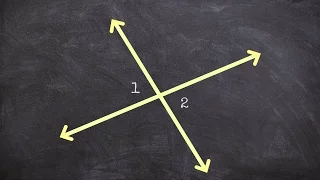
What are examples of Vertical angles

👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a

From playlist Angle Relationships

What is an example of lines that are a linear pair

From playlist Angle Relationships

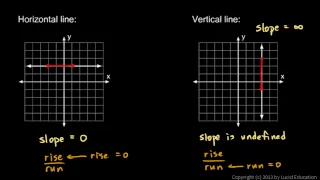
Algebra 1 8.04d - Horizontal and Vertical Lines

Two special cases of the slope of a line: A horizontal line (slope = 0) and a vertical line (slope = infinity).

From playlist Algebra 1 Chapter 8 (Selected Videos)

Horizontal & Vertical Lines | Graphs | Maths | FuseSchool

Learn about graphs. In this second part introductory video we will look at the equation of horizontal lines and vertical lines. We will also have a quick look at two important diagonal lines. Vertical lines on a graph all have the same x-coordinate. This means they will have an x= equati

From playlist MATHS

Branimir Cacic, Classical gauge theory on quantum principalbundles

Noncommutative Geometry Seminar (Europe), 20 October 2021

From playlist Global Noncommutative Geometry Seminar (Europe)

What are vertical angles

From playlist Angle Relationships

What are vertical angles

From playlist Angle Relationships

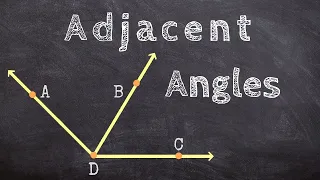
What are examples of adjacent angles

From playlist Angle Relationships

G. Molino - The Horizontal Einstein Property for H-Type sub-Riemannian Manifolds

We generalize the notion of H-type sub-Riemannian manifolds introduced by Baudoin and Kim, and then introduce a notion of parallel Clifford structure related to a recent work of Moroianu and Semmelmann. On those structures, we prove an Einstein property for the horizontal distribution usin

From playlist Journées Sous-Riemanniennes 2018

Vasily PESTUN - Multiplicative Higgs Bundles

From playlist Integrability, Anomalies and Quantum Field Theory

Bifurcating conformal metrics with constant Q-curvature - Renato Bettiol

More videos on http://video.ias.edu

From playlist Variational Methods in Geometry

Android Live - 2 | Android Layout Tutorial | Android Tutorial | Android Training | Edureka

🔥Edureka Android Certification Training: https://www.edureka.co/android-development-certification-course This Edureka video on "Android Layout Tutorial" will help you understand the Android Layout and how to work with them. Android Blog Series: http://bit.ly/2MJ6zbc Android Playlist her

From playlist Edureka Live Classes 2020

Verlinde Dimension Formula for the Space of Conformal Blocks and the moduli of G...V- Shrawan Kumar

Verlinde Dimension Formula Topic: Verlinde Dimension Formula for the Space of Conformal Blocks and the moduli of G-bundles V Speaker: Shrawan Kumar Affiliation: University of North Carolina; Member, School of Mathematics Date: November 17, 2022 Let G be a simply-connected complex semisim

From playlist Mathematics

Sheared Pleated surfaces and Limiting Configurations for Hitchin's equations by Michael Wolf

Surface Group Representations and Geometric Structures DATE: 27 November 2017 to 30 November 2017 VENUE:Ramanujan Lecture Hall, ICTS Bangalore The focus of this discussion meeting will be geometric aspects of the representation spaces of surface groups into semi-simple Lie groups. Classi

From playlist Surface Group Representations and Geometric Structures

Vertical and Horizontal Lines

Review and explanations of the slope of vertical and horizontal lines

From playlist Algebra

S. Diverio - Kobayashi hyperbolicity of complex projective manifolds and foliations (Part 4)

The aim of this mini course is to highlight some links between the study of the Kobayashi hyperbolicity properties of complex projective manifolds and holomorphic foliations. A compact complex space is Kobayashi hyperbolic if and only if every holomorphic map from the complex plane to it

From playlist Ecole d'été 2019 - Foliations and algebraic geometry

Shades of h-principle in foliation theory - Gael Meigniez

Seminar in Analysis and Geometry Topic: Shades of h-principle in foliation theory Speaker: Gael Meigniez Affiliation: Aix-Marseille University; Member, School of Mathematics Date: October 12, 2021

From playlist Mathematics

Michael Wolf - Sheared Pleated surfaces and Limiting Configurations for Hitchin's equations

Michael Wolf Sheared Pleated surfaces and Limiting Configurations for Hitchin's equations A recent work by Mazzeo-Swoboda-Weiss-Witt describes a stratum of the frontier of the space of SL(2,C) surface group representations in terms of 'limiting configurations' which solve a degenerate ver

From playlist Maryland Analysis and Geometry Atelier

Can vertical angles be complementary

From playlist Angle Relationships

Vertical and horizontal bundles

Related pages