What are the Angle Relationships for Parallel Lines and a Transversal
👉 Learn about converse theorems of parallel lines and a transversal. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated i
From playlist Parallel Lines and a Transversal

What are parallel lines and a transversal
👉 Learn about converse theorems of parallel lines and a transversal. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated i
From playlist Parallel Lines and a Transversal
What is the Consecutive Interior Angle Converse Theorem
👉 Learn about converse theorems of parallel lines and a transversal. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated i
From playlist Parallel Lines and a Transversal

What is the Corresponding Angle Converse Theorem
👉 Learn about converse theorems of parallel lines and a transversal. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated i
From playlist Parallel Lines and a Transversal
Proving Parallel Lines with Angle Relationships
👉 Learn about converse theorems of parallel lines and a transversal. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated i
From playlist Parallel Lines and a Transversal
What is the Alternate Exterior Angle Converse Theorem
👉 Learn about converse theorems of parallel lines and a transversal. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated i
From playlist Parallel Lines and a Transversal

👉 Learn how to define and classify different angles based on their characteristics and relationships are given a diagram. The different types of angles that we will discuss will be acute, obtuse, right, adjacent, vertical, supplementary, complementary, and linear pair. The relationships
From playlist Angle Relationships From a Figure

[BOURBAKI 2019] Homology of Hurwitz spaces and the Cohen–Lenstra (...)- Randal-Williams - 15/06/19
Oscar RANDAL-WILLIAMS Homology of Hurwitz spaces and the Cohen–Lenstra heuristic for function fields, after Ellenberg, Venkatesh, and Westerland Ellenberg, Venkatesh, and Westerland have established a weak form of the function field analogue of the Cohen–Lenstra heuristic, on the distrib
From playlist BOURBAKI - 2019

Barcodes and C0 symplectic topology - Sobhan Seyfaddini
Symplectic Dynamics/Geometry Seminar Topic: Barcodes and C0 symplectic topology Speaker: Sobhan Seyfaddini Affiliation: ENS Paris Date: December 17, 2018 For more video please visit http://video.ias.edu
From playlist Variational Methods in Geometry

Danny Calegari: Big Mapping Class Groups - lecture 5
Part I - Theory : In the "theory" part of this mini-course, we will present recent objects and phenomena related to the study of big mapping class groups. In particular, we will define two faithful actions of some big mapping class groups. The first is an action by isometries on a Gromov-h
From playlist Topology
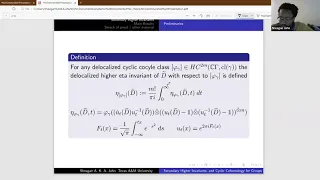
Sheagan John: Secondary higher invariants, and cyclic cohomology for groups of polynomial growth
Talk by Sheagan John in Global Noncommutative Geometry Seminar (Americas) http://www.math.wustl.edu/~xtang/NCG-Seminar.html on December 2, 2020.
From playlist Global Noncommutative Geometry Seminar (Americas)

Convex real projective structures on closed surfaces (Lecture 02) by Tengren Zhang
DISCUSSION MEETING SURFACE GROUP REPRESENTATIONS AND PROJECTIVE STRUCTURES ORGANIZERS: Krishnendu Gongopadhyay, Subhojoy Gupta, Francois Labourie, Mahan Mj and Pranab Sardar DATE: 10 December 2018 to 21 December 2018 VENUE: Ramanujan Lecture Hall, ICTS Bangalore The study of spaces o
From playlist Surface group representations and Projective Structures (2018)

Determining if two angles are adjacent or not
👉 Learn how to define and classify different angles based on their characteristics and relationships are given a diagram. The different types of angles that we will discuss will be acute, obtuse, right, adjacent, vertical, supplementary, complementary, and linear pair. The relationships
From playlist Angle Relationships From a Figure

Dyon degeneracies from Moonshine by Justin David
Bangalore Area Strings Meeting - 2017 TIME : 31 July 2017 to 02 August 2017 VENUE:Madhava Lecture Hall, ICTS Bangalore Bengaluru now has a large group of string theorists, with 9 faculty members in the area, between ICTS and IISc. This is apart from a large group of postdocs and graduate
From playlist Bangalore Area Strings Meeting - 2017
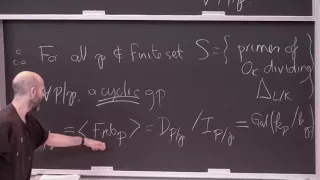
Kevin Buzzard (lecture 11/20) Automorphic Forms And The Langlands Program [2017]
Full course playlist: https://www.youtube.com/playlist?list=PLhsb6tmzSpiysoRR0bZozub-MM0k3mdFR http://wwwf.imperial.ac.uk/~buzzard/MSRI/ Summer Graduate School Automorphic Forms and the Langlands Program July 24, 2017 - August 04, 2017 Kevin Buzzard (Imperial College, London) https://w
From playlist MSRI Summer School: Automorphic Forms And The Langlands Program, by Kevin Buzzard [2017]

Some questions around quasi-periodic dynamics – Bassam Fayad & Raphaël Krikorian – ICM2018
Dynamical Systems and Ordinary Differential Equations Invited Lecture 9.2 Some questions around quasi-periodic dynamics Bassam Fayad & Raphaël Krikorian Abstract: We propose in these notes a list of some old and new questions related to quasi-periodic dynamics. A main aspect of quasi-per
From playlist Dynamical Systems and ODE

A brief introduction to sofic entropy theory – Lewis Bowen – ICM2018
Analysis and Operator Algebras | Dynamical Systems and Ordinary Differential Equations Invited Lecture 8.15 | 9.16 A brief introduction to sofic entropy theory Lewis Bowen Abstract: Sofic entropy theory is a generalization of the classical Kolmogorov–Sinai entropy theory to actions of a
From playlist Dynamical Systems and ODE

What is an angle and it's parts
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships
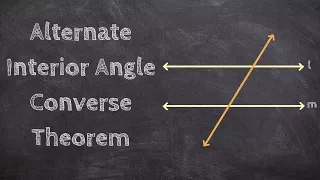
What is the Alternate Interior Angle Converse Theorem
👉 Learn about converse theorems of parallel lines and a transversal. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated i
From playlist Parallel Lines and a Transversal

Convex real projective structures on closed surfaces (Lecture 01) by Tengren Zhang
DISCUSSION MEETING SURFACE GROUP REPRESENTATIONS AND PROJECTIVE STRUCTURES ORGANIZERS: Krishnendu Gongopadhyay, Subhojoy Gupta, Francois Labourie, Mahan Mj and Pranab Sardar DATE: 10 December 2018 to 21 December 2018 VENUE: Ramanujan Lecture Hall, ICTS Bangalore The study of spaces o
From playlist Surface group representations and Projective Structures (2018)