
Introduction to Metric Spaces - Definition of a Metric. - The metric on R - The Euclidean Metric on R^n - A metric on the set of all bounded functions - The discrete metric
From playlist Topology

👉 Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes

Spectrum of Hg Lamp / amazing science experiment
Identify the spectral lines of Hg lamp Enjoy the amazing colors! Music: https://www.bensound.com/
From playlist Optics

Introduction to Projective Geometry (Part 1)
The first video in a series on projective geometry. We discuss the motivation for studying projective planes, and list the axioms of affine planes.
From playlist Introduction to Projective Geometry
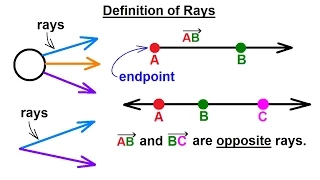
Geometry - Basic Terminology (4 of 28) Definition of Rays
Visit http://ilectureonline.com for more math and science lectures! In this video I will define and give examples of what are rays. Next video in the Basic Terminology series can be seen at: http://youtu.be/FI68xoUogoM
From playlist GEOMETRY 1 - BASIC TERMINOLOGY
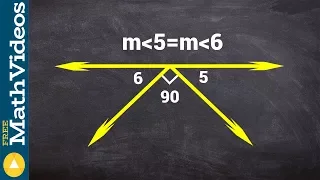
Determine the values of two angles that lie on a lie with a third angle
👉 Learn how to define and classify different angles based on their characteristics and relationships are given a diagram. The different types of angles that we will discuss will be acute, obtuse, right, adjacent, vertical, supplementary, complementary, and linear pair. The relationships
From playlist Angle Relationships From a Figure

What is the definition of a ray
👉 Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes

Lisa Glaser: A picture of a spectral triple
Talk at the conference "Noncommutative geometry meets topological recursion", August 2021, University of Münster. Abstract: A compact manifold can be described through a spectral triple, consisting of a Hilbert space H, an algebra of functions A and a Dirac operator D. But what if we are g
From playlist Noncommutative geometry meets topological recursion 2021

Identify the spectral lines of Mercury light by a coarse diffraction grating
Enjoy! Music: https://www.bensound.com/royalty-free-music
From playlist Optics
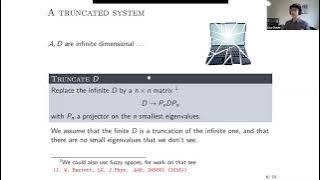
Lisa Glaser: Truncated spectral triples on the computer
Talk by Lisa Glaser in Global Noncommutative Geometry Seminar (Europe) http://www.noncommutativegeometry.nl/ncgseminar/ on February 2, 2021
From playlist Global Noncommutative Geometry Seminar (Europe)

Roberta Iseppi: The BV-BRST cohomology for U(n)-gauge theories induced by finitespectral triples
Talk at the conference "Noncommutative geometry meets topological recursion", August 2021, University of Münster. Abstract: The Batalin–Vilkovisky (BV) formalism provides a cohomological approach for the study of gauge symmetries: given a gauge theory, by introducing extra (non-existing) f
From playlist Noncommutative geometry meets topological recursion 2021
Alain Connes: On the Notion of Space
Talk by Alain Connes in Global Noncommutative Geometry Seminar (Americas) https://globalncgseminar.org/talks/3573/ on September 3, 2021.
From playlist Global Noncommutative Geometry Seminar (Americas)

Walter van Suijlekom: Non-commutative geometry and spectral triples - Lecture 1
Mini course of the conference "Noncommutative geometry meets topological recursion", August 2021, University of Münster. Abstract: Our starting point is a spectral approach to geometry, starting with the simple ques tion ’can one hear the shape of a drum’. This was phrased by Mark Kac in t
From playlist Noncommutative geometry meets topological recursion 2021

Local Talk: "Blowing up bubbles into minimal surfaces", Emma Carberry
SMRI -MATRIX Symposium: Nijenhuis Geometry and Integrable Systems Week 2 (MATRIX): Local Talk by Emma Carberry 18 February 2022 ---------------------------------------------------------------------------------------------------------------------- SMRI-MATRIX Joint Symposium, 7 – 18 Febru
From playlist MATRIX-SMRI Symposium: Nijenhuis Geometry and integrable systems

Spectrum and abnormals in sub-Riemannian geometry: the 4D quasi-contact case - Nikhil Savale
Symplectic Dynamics/Geometry Seminar Topic: Spectrum and abnormals in sub-Riemannian geometry: the 4D quasi-contact case Speaker: Nikhil Savale Affiliation: University of Cologne Date: October 28, 2019 For more video please visit http://video.ias.edu
From playlist Mathematics

Spectral geometry on metric graphs - Lior Alon
Short Talks by Postdoctoral Members Topic: Spectral geometry on metric graphs Speaker: Lior Alon Affiliation: Member, School of Mathematics Date: September 22, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Masoud Khalkhali: Newton divided differences, higher curved quantum tori, and scalar curvature
Talk by Masoud Khalkhali in Global Noncommutative Geometry Seminar (Americas) http://www.math.wustl.edu/~xtang/NCG-Seminar.html on July 25, 2020.
From playlist Global Noncommutative Geometry Seminar (Americas)
Angle-Angle Triangle Similarity Theorem: Dynamic Proof
Link: https://www.geogebra.org/m/Q8EYTUK2
From playlist Geometry: Dynamic Interactives!

Christian Liedtke: Crystalline cohomology, period maps, and applications to K3 surfaces
Abstract: I will first introduce K3 surfaces and determine their algebraic deRham cohomology. Next, we will see that crystalline cohomology (no prior knowledge assumed) is the "right" replacement for singular cohomology in positive characteristic. Then, we will look at one particular class
From playlist Algebraic and Complex Geometry
