
Statistics 4 Measures of Dispersion.mov
Discussing range, variance, and standard deviation as measures of dispersion.
From playlist Medical Statistics

What is an enlargement dilation
👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations

WHAT ARE SHRINK RULES Short #16 tubalcain patternmakers
You are watching #16 of my "SHORT SUBJECT" video series. Here is a link to my SHORT SUBJECT PLAYLIST-- https://www.youtube.com/playlist?list=PL6HIFled82YXOnt4YhGvYPBQ40XO3ITRk Please like & subscribe & watch my 1400 other machine shop videos. #dialindicator#testindicator#brown&sharpe#mitut
From playlist SHORT SUBJECTS
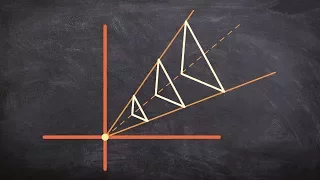
What are dilations, similarity and scale factors
👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations

Determining the scale factor of the enlargement of a triangle
👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations

How to determine the ratio of a reduction dilation
👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations

👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations
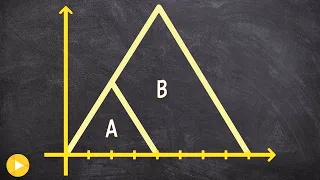
How to determine the scale factor of a dilation for enlargement
👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations

Statistical Rethinking Winter 2019 Lecture 15
Lecture 15 of the Dec 2018 through March 2019 edition of Statistical Rethinking: A Bayesian Course with R and Stan. Covers Chapter 13, Multilevel Models.
From playlist Statistical Rethinking Winter 2019

Statistical Rethinking - Lecture 17
Lecture 17 - Multilevel models (2) - Statistical Rethinking: A Bayesian Course with R Examples
From playlist Statistical Rethinking Winter 2015

Daniel Yekutieli: Hierarchical Bayes Modeling for Large-Scale Inference
CIRM VIRTUAL EVENT Recorded during the meeting "Mathematical Methods of Modern Statistics 2" the June 03, 2020 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians
From playlist Virtual Conference

Statistical Rethinking - Lecture 20
Lecture 20 - Measurement error, missing data imputation, false-positive science - Statistical Rethinking: A Bayesian Course with R Examples
From playlist Statistical Rethinking Winter 2015

How to determine the reduction scale factor for two parallelograms
👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations

Statistical Rethinking Fall 2017 - week08 lecture14
Week 08, lecture 14 for Statistical Rethinking: A Bayesian Course with Examples in R and Stan, taught at MPI-EVA in Fall 2017. This lecture covers Chapter 12. Slides are available here: https://speakerdeck.com/rmcelreath/statistical-rethinking-fall-2017-lecture-14 Additional informatio
From playlist Statistical Rethinking Fall 2017

Statistical Rethinking Winter 2019 Lecture 17
Lecture 17 of the Dec 2018 through March 2019 edition of Statistical Rethinking: A Bayesian Course with R and Stan. Introduction to varying slopes and covariance priors.
From playlist Statistical Rethinking Winter 2019
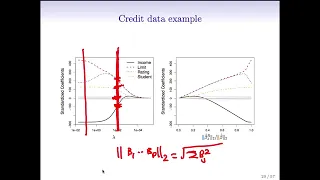
Statistical Learning: 6.6 Shrinkage methods and ridge regression
Statistical Learning, featuring Deep Learning, Survival Analysis and Multiple Testing You are able to take Statistical Learning as an online course on EdX, and you are able to choose a verified path and get a certificate for its completion: https://www.edx.org/course/statistical-learning
From playlist Statistical Learning
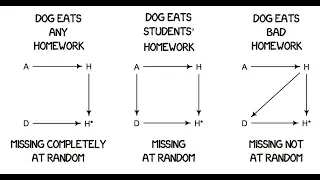
Statistical Rethinking Winter 2019 Lecture 20
Lecture 20 of the Dec 2018 through March 2019 edition of Statistical Rethinking: A Bayesian Course with R and Stan. Covers Chapter 15, measurement error and missing data imputation.
From playlist Statistical Rethinking Winter 2019

Statistical Rethinking Fall 2017 - week09 lecture16
Week 09, lecture 16 for Statistical Rethinking: A Bayesian Course with Examples in R and Stan, taught at MPI-EVA in Fall 2017. This lecture covers Chapter 13. Slides are available here: https://speakerdeck.com/rmcelreath/statistical-rethinking-fall-2017-lecture-16 Additional informatio
From playlist Statistical Rethinking Fall 2017

Determining the scale factor of two quadrilaterals
👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations

The weirdest paradox in statistics (and machine learning)
🌏 AD: Get Exclusive NordVPN deal here ➼ https://nordvpn.com/mathemaniac. It's risk-free with Nord's 30-day money-back guarantee! ✌ Second channel video: https://www.youtube.com/watch?v=3ne9yghOtw8 Stein's paradox is of fundamental importance in modern statistics, introducing concepts of
From playlist Novel topics (not in usual math curricula)