
Find the reference angle of a angle larger than 2pi
👉 Learn how to find the reference angle of a given angle. The reference angle is the acute angle formed by the terminal side of an angle and the x-axis. To find the reference angle, we determine the quadrant on which the given angle lies and use the reference angle formula for the quadrant
From playlist Find the Reference Angle

Learning to find the reference angle by using coterminal angle
👉 Learn how to find the reference angle of a given angle. The reference angle is the acute angle formed by the terminal side of an angle and the x-axis. To find the reference angle, we determine the quadrant on which the given angle lies and use the reference angle formula for the quadrant
From playlist Find the Reference Angle
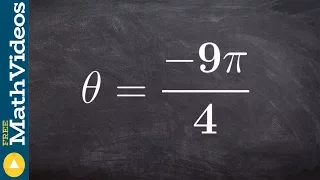
How to find the reference angle of an angle larger than 2pi
👉 Learn how to find the reference angle of a given angle. The reference angle is the acute angle formed by the terminal side of an angle and the x-axis. To find the reference angle, we determine the quadrant on which the given angle lies and use the reference angle formula for the quadrant
From playlist Find the Reference Angle
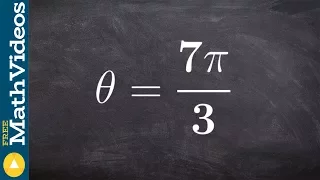
Sketch the angle then find the reference angle
👉 Learn how to find the reference angle of a given angle. The reference angle is the acute angle formed by the terminal side of an angle and the x-axis. To find the reference angle, we determine the quadrant on which the given angle lies and use the reference angle formula for the quadrant
From playlist Find the Reference Angle

Learn how to determine the reference angle of an angle in terms of pi
👉 Learn how to find the reference angle of a given angle. The reference angle is the acute angle formed by the terminal side of an angle and the x-axis. To find the reference angle, we determine the quadrant on which the given angle lies and use the reference angle formula for the quadrant
From playlist Find the Reference Angle
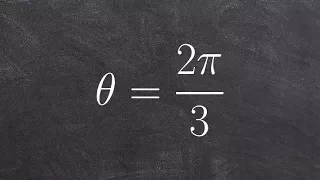
Finding the reference angle of an angle in quadrant two
👉 Learn how to find the reference angle of a given angle. The reference angle is the acute angle formed by the terminal side of an angle and the x-axis. To find the reference angle, we determine the quadrant on which the given angle lies and use the reference angle formula for the quadrant
From playlist Find the Reference Angle

Quick tips for setting up a line in desmos from a point and slope
From playlist desmos

F. Andreatta - The height of CM points on orthogonal Shimura varieties and Colmez conjecture (part4)
We will first introduce Shimura varieties of orthogonal type, their Heegner divisors and some special points, called CM (Complex Multiplication) points. Secondly we will review conjectures of Bruinier-Yang and Buinier-Kudla-Yang which provide explicit formulas for the arithmetic intersecti
From playlist Ecole d'été 2017 - Géométrie d'Arakelov et applications diophantiennes

How to determine the reference angle of an angle in degrees
👉 Learn how to find the reference angle of a given angle. The reference angle is the acute angle formed by the terminal side of an angle and the x-axis. To find the reference angle, we determine the quadrant on which the given angle lies and use the reference angle formula for the quadrant
From playlist Find the Reference Angle

F. Andreatta - The height of CM points on orthogonal Shimura varieties and Colmez conjecture (part2)
We will first introduce Shimura varieties of orthogonal type, their Heegner divisors and some special points, called CM (Complex Multiplication) points. Secondly we will review conjectures of Bruinier-Yang and Buinier-Kudla-Yang which provide explicit formulas for the arithmetic intersecti
From playlist Ecole d'été 2017 - Géométrie d'Arakelov et applications diophantiennes

In an attempt to create something pretty to look at that people are familiar with, I applied techniques I've learned to the Minecraft rendering pipeline. Code: https://github.com/GarrettGunnell/Minecraft-Shaders Twitter: https://twitter.com/Acerola_t Twitch: https://www.twitch.tv/acerola
From playlist Main Series

Thomas KAPPELER - Analytic extensions of frequencies of integrable PDEs and applications
In form of a case study for the mKdV and the KdV2 equation we discuss a novel approach of representing frequencies of integrable PDEs which allows to extend them analytically to spaces of low regularity and to study their asymptotics. Applications include properties of the actions to frequ
From playlist Trimestre "Ondes Non linéaires" - June Conference

The Four-Color Theorem and an Instanton Invariant for Spatial Graphs I - Peter Kronheimer
Peter Kronheimer Harvard University October 13, 2015 http://www.math.ias.edu/seminars/abstract?event=83214 Given a trivalent graph embedded in 3-space, we associate to it an instanton homology group, which is a finite-dimensional Z/2 vector space. The main result about the instanton hom
From playlist Geometric Structures on 3-manifolds

A stacky approach to crystalline (and prismatic) cohomology - Vladimir Drinfeld
Joint IAS/Princeton University Number Theory Seminar Topic: A stacky approach to crystalline (and prismatic) cohomology Speaker: Vladimir Drinfeld Affiliation: The University of Chicago; Visiting Professor, School of Mathematics Date: October 3, 2019 For more video please visit http://vi
From playlist Mathematics

Fixing The Graphics Of FINAL FANTASY XIV
I've spent the past two months hard at work developing ReShade and GShade shaders to improve the graphics of Final Fantasy XIV. In this video I go over my creative and developmental process from start to finish explaining the decisions I made, the major issues I came across and the theory
From playlist Render Repair

Foliations on Unitary Shimura Varieties in Characteristic p by Ehud De Shalit
PERFECTOID SPACES ORGANIZERS: Debargha Banerjee, Denis Benois, Chitrabhanu Chaudhuri, and Narasimha Kumar Cheraku DATE & TIME: 09 September 2019 to 20 September 2019 VENUE: Madhava Lecture Hall, ICTS, Bangalore Scientific committee: Jacques Tilouine (University of Paris, France) Eknath
From playlist Perfectoid Spaces 2019

Find the reference angle and sketch both angles in standard position
👉 Learn how to find the reference angle of a given angle. The reference angle is the acute angle formed by the terminal side of an angle and the x-axis. To find the reference angle, we determine the quadrant on which the given angle lies and use the reference angle formula for the quadrant
From playlist Find the Reference Angle
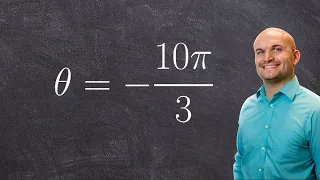
Find the reference angle and sketch both angles in standard position
👉 Learn how to find the reference angle of a given angle. The reference angle is the acute angle formed by the terminal side of an angle and the x-axis. To find the reference angle, we determine the quadrant on which the given angle lies and use the reference angle formula for the quadrant
From playlist Find the Reference Angle
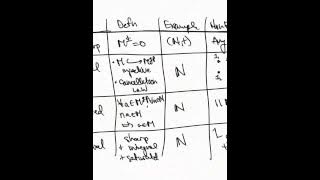
Geometry of Frobenioids - part 2 - (Set) Monoids
This is an introduction to the basic properties of Monoids. This video intended to be a starting place for log-schemes, Mochizuki's IUT or other absolute geometric constructions using monoids.
From playlist Geometry of Frobenioids
