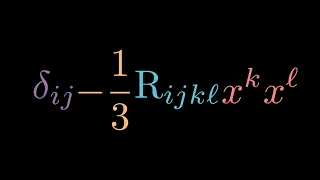
Curvature of a Riemannian Manifold | Riemannian Geometry
In this lecture, we define the exponential mapping, the Riemannian curvature tensor, Ricci curvature tensor, and scalar curvature. The focus is on an intuitive explanation of the curvature tensors. The curvature tensor of a Riemannian metric is a very large stumbling block for many student
From playlist All Videos

Understanding and computing the Riemann zeta function
In this video I explain Riemann's zeta function and the Riemann hypothesis. I also implement and algorithm to compute the return values - here's the Python script:https://gist.github.com/Nikolaj-K/996dba1ff1045d767b10d4d07b1b032f
From playlist Programming

Riemann Sum Defined w/ 2 Limit of Sums Examples Calculus 1
I show how the Definition of Area of a Plane is a special case of the Riemann Sum. When finding the area of a plane bound by a function and an axis on a closed interval, the width of the partitions (probably rectangles) does not have to be equal. I work through two examples that are rela
From playlist Calculus
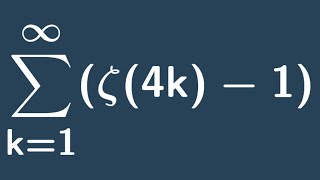
More identities involving the Riemann-Zeta function!
By applying some combinatorial tricks to an identity from https://youtu.be/2W2Ghi9idxM we are able to derive two identities involving the Riemann-Zeta function. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist The Riemann Zeta Function

Some identities involving the Riemann-Zeta function.
After introducing the Riemann-Zeta function we derive a generating function for its values at positive even integers. This generating function is used to prove two sum identities. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist The Riemann Zeta Function

Lagrangian Floer theory (Lecture – 02) by Sushmita Venugopalan
J-Holomorphic Curves and Gromov-Witten Invariants DATE:25 December 2017 to 04 January 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore Holomorphic curves are a central object of study in complex algebraic geometry. Such curves are meaningful even when the target has an almost complex stru
From playlist J-Holomorphic Curves and Gromov-Witten Invariants

Lagrangian Floer theory by Sushmita Venugopalan
J-Holomorphic Curves and Gromov-Witten Invariants DATE:25 December 2017 to 04 January 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore Holomorphic curves are a central object of study in complex algebraic geometry. Such curves are meaningful even when the target has an almost complex stru
From playlist J-Holomorphic Curves and Gromov-Witten Invariants

Behavior of Welschinger Invariants Under Morse Simplification - Erwan Brugalle
Erwan Brugalle Universite de Paris 6 November 9, 2012 Welschinger invariants, real analogs of genus 0 Gromov-Witten invariants, provide non-trivial lower bounds in real algebraic geometry. In this talk I will explain how to get some wall-crossing formulas relating Welschinger invariants o
From playlist Mathematics

What is the Riemann Hypothesis?
This video provides a basic introduction to the Riemann Hypothesis based on the the superb book 'Prime Obsession' by John Derbyshire. Along the way I look at convergent and divergent series, Euler's famous solution to the Basel problem, and the Riemann-Zeta function. Analytic continuation
From playlist Mathematics

What is General Relativity? Lesson 49: Constructing the Weyl tensor I
What is General Relativity? Lesson 49: Constructing the Weyl tensor I We calculate the conformally invariant part of the Riemann tensor. This is a complex calculation that is not generally done in textbooks. The motivation for the Weyl tensor will come in a later lesson, but I think the d
From playlist What is General Relativity?

Homological Mirror Symmetry - Nicholas Sheridan
Nicholas Sheridan Massachusetts Institute of Technology; Member, School of Mathematics February 11, 2013 Mirror symmetry is a deep conjectural relationship between complex and symplectic geometry. It was first noticed by string theorists. Mathematicians became interested in it when string
From playlist Mathematics

Tensor Calculus Lecture 8e: The Riemann Christoffel Tensor & Gauss's Remarkable Theorem
This course will eventually continue on Patreon at http://bit.ly/PavelPatreon Textbook: http://bit.ly/ITCYTNew Errata: http://bit.ly/ITAErrata McConnell's classic: http://bit.ly/MCTensors Table of Contents of http://bit.ly/ITCYTNew Rules of the Game Coordinate Systems and the Role of Te
From playlist Introduction to Tensor Calculus

An introduction to spectral data for Higgs bundles.. by Laura Schaposnik
Higgs bundles URL: http://www.icts.res.in/program/hb2016 DATES: Monday 21 Mar, 2016 - Friday 01 Apr, 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore DESCRIPTION: Higgs bundles arise as solutions to noncompact analog of the Yang-Mills equation. Hitchin showed that irreducible solutio
From playlist Higgs Bundles

Generalized Geometry for String Theory - B. Zwiebach - 12/10/2013
A conference celebrating the 50th anniversary of quarks honoring Murray Gell-Mann was held at Caltech on December 9-10, 2013. For more information, visit: http://hep.caltech.edu/gm/
From playlist String Theory - Prof. Zwiebach & Susskind

Transversality and super-rigidity in Gromov-Witten Theory by Chris Wendl
J-Holomorphic Curves and Gromov-Witten Invariants DATE:25 December 2017 to 04 January 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore Holomorphic curves are a central object of study in complex algebraic geometry. Such curves are meaningful even when the target has an almost complex stru
From playlist J-Holomorphic Curves and Gromov-Witten Invariants

Weil conjectures 2: Functional equation
This is the second lecture about the Weil conjectures. We show that the Riemann-Roch theorem implies the rationality and functional equation of the zeta function of a curve over a finite field.
From playlist Algebraic geometry: extra topics

Algebraic geometry 44: Survey of curves
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It gives an informal survey of complex curves of small genus.
From playlist Algebraic geometry I: Varieties
What is General Relativity? Lesson 50: Constructing the Weyl Tensor II
What is General Relativity? Lesson 50: Constructing the Weyl Tensor II We calculate the traceless part of the Riemann tensor. We will discover that the result is the same as the calculation of the conformally invariant part discovered in Lesson 49! This begins a diversion into understand
From playlist What is General Relativity?

MATH331: Riemann Surfaces - part 1
We define what a Riemann Surface is. We show that PP^1 is a Riemann surface an then interpret our crazy looking conditions from a previous video about "holomorphicity at infinity" as coming from the definition of a Riemann Surface.
From playlist The Riemann Sphere

Transversality and super-rigidity in Gromov-Witten Theory (Lecture - 04) by Chris Wendl
J-Holomorphic Curves and Gromov-Witten Invariants DATE:25 December 2017 to 04 January 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore Holomorphic curves are a central object of study in complex algebraic geometry. Such curves are meaningful even when the target has an almost complex stru
From playlist J-Holomorphic Curves and Gromov-Witten Invariants