
R. Bamler - Compactness and partial regularity theory of Ricci flows in higher dimensions (vt)
We present a new compactness theory of Ricci flows. This theory states that any sequence of Ricci flows that is pointed in an appropriate sense, subsequentially converges to a synthetic flow. Under a natural non-collapsing condition, this limiting flow is smooth on the complement of a sing
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Nicol Gigli - 22 September 2016
Gigli, Nicola "Spaces with Ricci curvature bounded from below: state of the art and future challenges."
From playlist A Mathematical Tribute to Ennio De Giorgi

T. Richard - Lower bounds on Ricci curvature, with a glimpse on limit spaces (Part 4)
The goal of these lectures is to introduce some fundamental tools in the study of manifolds with a lower bound on Ricci curvature. We will first state and prove the laplacian comparison theorem for manifolds with a lower bound on the Ricci curvature, and derive some important consequences
From playlist Ecole d'été 2016 - Analyse géométrique, géométrie des espaces métriques et topologie

T. Richard - Lower bounds on Ricci curvature, with a glimpse on limit spaces (Part 2)
The goal of these lectures is to introduce some fundamental tools in the study of manifolds with a lower bound on Ricci curvature. We will first state and prove the laplacian comparison theorem for manifolds with a lower bound on the Ricci curvature, and derive some important consequences
From playlist Ecole d'été 2016 - Analyse géométrique, géométrie des espaces métriques et topologie

T. Richard - Lower bounds on Ricci curvature, with a glimpse on limit spaces (Part 1)
The goal of these lectures is to introduce some fundamental tools in the study of manifolds with a lower bound on Ricci curvature. We will first state and prove the laplacian comparison theorem for manifolds with a lower bound on the Ricci curvature, and derive some important consequences
From playlist Ecole d'été 2016 - Analyse géométrique, géométrie des espaces métriques et topologie

T. Richard - Lower bounds on Ricci curvature, with a glimpse on limit spaces (Part 3)
The goal of these lectures is to introduce some fundamental tools in the study of manifolds with a lower bound on Ricci curvature. We will first state and prove the laplacian comparison theorem for manifolds with a lower bound on the Ricci curvature, and derive some important consequences
From playlist Ecole d'été 2016 - Analyse géométrique, géométrie des espaces métriques et topologie

T. Richard - Lower bounds on Ricci curvature, with a glimpse on limit spaces (Part 5)
The goal of these lectures is to introduce some fundamental tools in the study of manifolds with a lower bound on Ricci curvature. We will first state and prove the laplacian comparison theorem for manifolds with a lower bound on the Ricci curvature, and derive some important consequences
From playlist Ecole d'été 2016 - Analyse géométrique, géométrie des espaces métriques et topologie

Geometric Measure Theory on non smooth spaces with lower Ricci curvature bounds - Daniele Semola
Analysis & Mathematical Physics Topic: Geometric Measure Theory on non smooth spaces with lower Ricci curvature bounds Speaker: Daniele Semola Affiliation: Fields Institute, Toronto Date: November 02, 2022 There is a celebrated connection between minimal (or constant mean curvature) hype
From playlist Mathematics

Comparison geometry for Ricci curvature I, Guofang Wei [2016]
Slides for this talk: https://drive.google.com/open?id=1d3IhMz2enIsBOuKRPA6JF80FPqbHSR9v Ricci curvature occurs in the Einstein equation, Ricci flow, optimal transport, and is important both in mathematics and physics. Comparison method is one of the key tools in studying the Ricci curvat
From playlist Mathematics

Colloquium MathAlp 2019 - Claude Lebrun
Claude Lebrun - Mass, Scalar Curvature, Kähler Geometry, and All That Given a complete Riemannian manifold that looks enough like Euclidean space at infinity, physicists have defined a quantity called the “mass” that measures the asymptotic deviation of the geometry from the Euclidean mod
From playlist Colloquiums MathAlp

The Kahler-Ricci flow, Ricci-flat metrics and collapsing limits - Ben Weinkove [2015]
Name: Ben Weinkove Event: Workshop: Collapsing Calabi-Yau Manifolds Event URL: view webpage Title: The Kahler-Ricci flow, Ricci-flat metrics and collapsing limits Date: 2015-09-02 @2:15 PM Location: 102 Abstract: I will discuss the behavior of collapsing metrics on holomorphic fiber spac
From playlist Mathematics

Heather Macbeth: Kähler-Ricci solitons on crepant resolutions of finite quotients of C^n
Abstract: By a gluing construction, we produce steady Kähler-Ricci solitons on equivariant crepant resolutions of ℂ^n/GCn/G, where GG is a finite subgroup of SU(n)SU(n), generalizing Cao’s construction of such a soliton on a resolution of ℂ^n/ℤnCn/Zn. This is joint work with Olivier Biquar
From playlist Algebraic and Complex Geometry

Ricci flows with Rough Initial Data - Peter Topping
Workshop on Geometric Functionals: Analysis and Applications Topic: Ricci flows with Rough Initial Data Speaker: Peter Topping Affiliation: University of Warwick Date: March 8, 2019 For more video please visit http://video.ias.edu
From playlist Mathematics

Simon Donaldson | Applications of the Hormander technique in Kahler-Einstein geometry | 2012
Created: 2012-04-24 09:46 Collection: Workshop on Kahler Geometry Publisher: University of Cambridge Language: eng (English) Author: Simon Donaldson https://www.sms.cam.ac.uk/media/1247397
From playlist Mathematics
Christina Sormani: A Course on Intrinsic Flat Convergence part 4
The lecture was held within the framework of the Hausdorff Trimester Program: Optimal Transportation and the Workshop: Winter School & Workshop: New developments in Optimal Transport, Geometry and Analysis
From playlist HIM Lectures 2015

Conformal gap theorems of $S^4$ and $CP^2$ - Alice Chang [2017]
slides for this talk: https://drive.google.com/file/d/1d6Vzy5Rp3s2vZe0CWfr7nnwK5kG0RO_C/view?usp=sharing Name: Alice Chang Event: Workshop: Geometry of Manifolds Event URL: view webpage Title: Conformal gap theorems of $S^4$ and $CP^2$ Date: 2017-10-25 @9:30 AM Location: 102 Download the
From playlist Mathematics

GPDE Workshop Some Rigidity Results Using Full Non Linear Equations Djadli hi
Zindine Djadli University of France, Grenoble February 26, 2009 For more videos, visit http://video.ias.edu
From playlist Mathematics
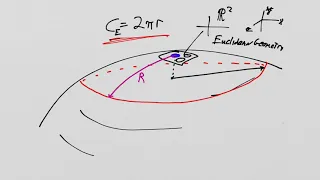
What is General Relativity? Lesson 59: Scalar Curvature Part 8: Interpretation of Scalar Curvature.
What is General Relativity? Lesson 59: Scalar Curvature Part 8: Interpretation of Scalar Curvature (note: this is a re-post of a video that was posted at 2x playback speed. Sorry!) We begin our examination of Section 4.4.6 of "A Simple Introduction to Particle Physics Part II - Geometric
From playlist What is General Relativity?
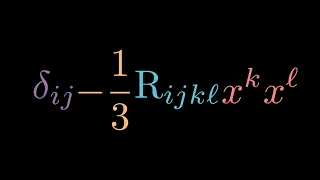
Curvature of a Riemannian Manifold | Riemannian Geometry
In this lecture, we define the exponential mapping, the Riemannian curvature tensor, Ricci curvature tensor, and scalar curvature. The focus is on an intuitive explanation of the curvature tensors. The curvature tensor of a Riemannian metric is a very large stumbling block for many student
From playlist All Videos

Cédric Villani - 3/7 La théorie synthétique de la courbure de Ricci
A la fin des années 90, les liens entre transport optimal, entropie et courbure de Ricci étaient mis au jour (Jordan-Kinderlehrer-Otto, Otto-Villani); quelques années plus tard, ce liens étaient exploités pour démarrer l'étude systématique du "point de vue synthétique" de la courbure de Ri
From playlist Cédric Villani - La théorie synthétique de la courbure de Ricci