
Maximum modulus principle In this video, I talk about the maximum modulus principle, which says that the maximum of the modulus of a complex function is attained on the boundary. I also show that the same thing is true for the real and imaginary parts, and finally I discuss the strong max
From playlist Complex Analysis
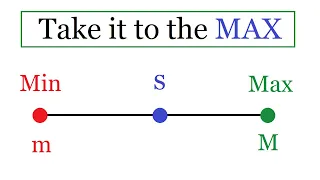
Maximum and Minimum of a set In this video, I define the maximum and minimum of a set, and show that they don't always exist. Enjoy! Check out my Real Numbers Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmCZggpJZvUXnUzaw7fHCtoh
From playlist Real Numbers

Free ebook https://bookboon.com/en/partial-differential-equations-ebook What is the maximum principle for partial differential equations and how is it useful? The main result is presented and proved. Such ideas have important applications to understanding the behaviour of solutions to pa
From playlist Partial differential equations

Maximum principle for heat equation In this video, I present the maximum principle, which is a very interesting property of the heat equation: Namely the largest (and smallest) value of solutions is attained either initially, or on the sides! Check out my PDE Playlist: https://www.yout
From playlist Partial Differential Equations
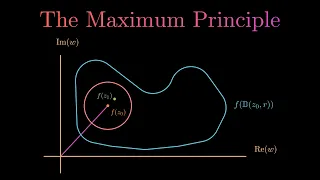
MAXIMUM PRINCIPLE -- Part 1 -- Core Theorems of Complex Analysis
Part 2: https://www.youtube.com/watch?v=jmP4VlgZvb0 Part 3: https://www.youtube.com/watch?v=fLnRDhhzWKQ In this video, we give a proof of the Maximum Principle, which is a monumental result in the subject of complex analysis. The maximum principle is also referred to as the maximum modul
From playlist Complex Analysis

Maximum and Minimum Values (Closed interval method)
A review of techniques for finding local and absolute extremes, including an application of the closed interval method
From playlist 241Fall13Ex3

Extreme Value Theorem Using Critical Points
Calculus: The Extreme Value Theorem for a continuous function f(x) on a closed interval [a, b] is given. Relative maximum and minimum values are defined, and a procedure is given for finding maximums and minimums. Examples given are f(x) = x^2 - 4x on the interval [-1, 3], and f(x) =
From playlist Calculus Pt 1: Limits and Derivatives

Optimal control of spin systems with applications in (...) - D. Sugny - Workshop 2 - CEB T2 2018
Dominique Sugny (Univ. Bourgogne) / 05.06.2018 Optimal control of spin systems with applications in Magnetic Resonance Optimal control can be viewed as a generalization of the classical calculus of variations for problems with dynamical constraints. Optimal control was born in its modern
From playlist 2018 - T2 - Measurement and Control of Quantum Systems: Theory and Experiments

Learning Optimal Control with Stochastic Models of Hamiltonian Dynamics for Shape & Function Optim.
Speaker: Chandrajit Bajaj (7/25/22) Abstract: Shape and Function Optimization can be achieved through Optimal Control over infinite-dimensional search space. All optimal control problems can be solved by first applying the Pontryagin maximum principle, and then computing a solution to the
From playlist Applied Geometry for Data Sciences 2022

Marc Levine: Refined enumerative geometry (Lecture 4)
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Lecture 4: Characteristic classes in Witt-cohomology Classical enumerative geometry relies heavily on the theory of Chern classes of vector bundles and the splitting principle, which
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Duality for Rabinowitz-Floer homology - Alex Oancea
IAS/PU-Montreal-Paris-Tel-Aviv Symplectic Geometry Topic: Duality for Rabinowitz-Floer homology Speaker: Alex Oancea Affiliation: Institut de Mathématiques de Jussieu-Paris Rive Gauche Date: May 27, 2020 For more video please visit http://video.ias.edu
From playlist PU/IAS Symplectic Geometry Seminar
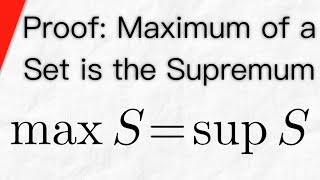
Proof: Maximum of a Set is the Supremum | Real Analysis
The maximum of a set is also the supremum of the set, we will prove this in today's lesson! This also applies to functions, since the range of a function is just a set of values. So if a function takes on a maximum value m, then the maximum m is also the supremum of the function. Recall
From playlist Real Analysis

F. Santambrogio - Optimal Control, Differential Games, Mean Field Games, ...
Optimal Control, Differential Games, Mean Field Games, and Pontryagin and Hamilton-Jacobi equations on probabilities The talk will be a short introduction to the emerging topic of Mean Field Games in connection with optimal control and differential games. I will present what is in general
From playlist Journées Sous-Riemanniennes 2017

3 Nandakumaran - An Introduction to deterministic optimal control and controllability
PROGRAM NAME :WINTER SCHOOL ON STOCHASTIC ANALYSIS AND CONTROL OF FLUID FLOW DATES Monday 03 Dec, 2012 - Thursday 20 Dec, 2012 VENUE School of Mathematics, Indian Institute of Science Education and Research, Thiruvananthapuram Stochastic analysis and control of fluid flow problems have
From playlist Winter School on Stochastic Analysis and Control of Fluid Flow

Calculus: Absolute Maximum and Minimum Values
In this video, we discuss how to find the absolute maximum and minimum values of a function on a closed interval.
From playlist Calculus
4 Nandakumaran - An Introduction to deterministic optimal control and controllability
PROGRAM NAME :WINTER SCHOOL ON STOCHASTIC ANALYSIS AND CONTROL OF FLUID FLOW DATES Monday 03 Dec, 2012 - Thursday 20 Dec, 2012 VENUE School of Mathematics, Indian Institute of Science Education and Research, Thiruvananthapuram Stochastic analysis and control of fluid flow problems have
From playlist Winter School on Stochastic Analysis and Control of Fluid Flow

Michael Hopkins: Bernoulli numbers, homotopy groups, and Milnor
Abstract: In his address at the 1958 International Congress of Mathematicians Milnor described his joint work with Kervaire, relating Bernoulli numbers, homotopy groups, and the theory of manifolds. These ideas soon led them to one of the most remarkable formulas in mathematics, relating f
From playlist Abel Lectures

Loop products, closed geodesics and self-intersections - Nancy Hingston
Workshop on Geometric Functionals: Analysis and Applications Topic: Loop products, closed geodesics and self-intersections Speaker: Nancy Hingston Affiliation: The College of New Jersey Date: March 6, 2019 For more video please visit http://video.ias.edu
From playlist Mathematics

Math 101 091317 Introduction to Analysis 06 Introduction to the Least Upper Bound Axiom
Definition of the maximum (minimum) of a set. Existence of maximum and minimum for finite sets. Definitions: upper bound of a set; bounded above; lower bound; bounded below; bounded. Supremum (least upper bound); infimum (greatest lower bound). Statement of Least Upper Bound Axiom (com
From playlist Course 6: Introduction to Analysis (Fall 2017)

Lecture 8 | MIT 6.832 Underactuated Robotics, Spring 2009
Lecture 8: Dynamic programming (DP) and policy search Instructor: Russell Tedrake See the complete course at: http://ocw.mit.edu/6-832s09 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.832 Underactuated Robotics, Spring 2009