
Definition of a Ring and Examples of Rings
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Ring and Examples of Rings - Definition of a Ring. - Definition of a commutative ring and a ring with identity. - Examples of Rings include: Z, Q, R, C under regular addition and multiplication The Ring of all n x
From playlist Abstract Algebra
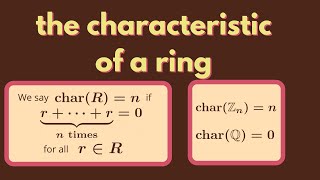
Abstract Algebra | The characteristic of a ring.
We define the characteristic of a ring and give some definitions. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Ring Theory: We define rings and give many examples. Items under consideration include commutativity and multiplicative inverses. Example include modular integers, square matrices, polynomial rings, quaternions, and adjoins of algebraic and transcendental numbers.
From playlist Abstract Algebra

Abstract Algebra | Polynomial Rings
We introduce the notion of a polynomial ring, give some examples, and prove a few classic results. In particular we prove that if R is an integral domain then R[x] is as well. http://www.michael-penn.net https://www.researchgate.net/profile/Michael_Penn5 http://www.randolphcollege.edu/mat
From playlist Abstract Algebra

RNT2.5. Polynomial Rings over Fields
Ring Theory: We show that polynomial rings over fields are Euclidean domains and explore factorization and extension fields using irreducible polynomials. As an application, we show that the units of a finite field form a cyclic group under multiplication.
From playlist Abstract Algebra

RNT1.4. Ideals and Quotient Rings
Ring Theory: We define ideals in rings as an analogue of normal subgroups in group theory. We give a correspondence between (two-sided) ideals and kernels of homomorphisms using quotient rings. We also state the First Isomorphism Theorem for Rings and give examples.
From playlist Abstract Algebra

Abstract Algebra | What is a ring?
We give the definition of a ring and present some examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

RNT1.2. Definition of Integral Domain
Ring Theory: We consider integral domains, which are commutative rings that contain no zero divisors. We show that this property is equivalent to a cancellation law for the ring. Finally we note some basic connections between integral domains and fields.
From playlist Abstract Algebra

Abstract Algebra | Types of rings.
We define several and give examples of different types of rings which have additional structure. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Georg Regensburger, University of Kassel
March 22, Georg Regensburger, University of Kassel Integro-differential operators with matrix coefficients
From playlist Spring 2022 Online Kolchin seminar in Differential Algebra
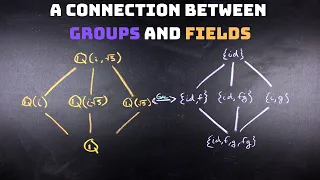
The Structure of Fields: What is a field and a connection between groups and fields
This video is primarily meant to help develop some ideas around the structure of fields and a connection between groups and fields (which will allow me to create more abstract algebra videos in the future! 😀😅🤓) 00:00 Intro 01:04 What is a Field? Here we give the definition of a field in
From playlist The New CHALKboard

Ring Examples (Abstract Algebra)
Rings are one of the key structures in Abstract Algebra. In this video we give lots of examples of rings: infinite rings, finite rings, commutative rings, noncommutative rings and more! Be sure to subscribe so you don't miss new lessons from Socratica: http://bit.ly/1ixuu9W ♦♦♦♦♦♦♦♦♦
From playlist Abstract Algebra

Commutative algebra 2 (Rings, ideals, modules)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. This lecture is a review of rings, ideals, and modules, where we give a few examples of non-commutative rings and rings without
From playlist Commutative algebra

Visual Group Theory, Lecture 7.2: Ideals, quotient rings, and finite fields
Visual Group Theory, Lecture 7.2: Ideals, quotient rings, and finite fields A left (resp., right) ideal of a ring R is a subring that is invariant under left (resp., right) multiplication. Two-sided ideals are those that are both left and right ideals. This is the analogue of normal subgr
From playlist Visual Group Theory

A Short Course in Algebra and Number Theory - Rings
To supplement a course taught at The University of Queensland's School of Mathematics and Physics I present a very brief summary of algebra and number theory for those students who need to quickly refresh that material or fill in some gaps in their understanding. This is the second lectu
From playlist A Short Course in Algebra and Number Theory

Rings and modules 2: Group rings
This lecture is part of an online course on rings and modules. We decribe some examples of rings constructed from groups and monoids, such as group rings and rings of Dirichlet polynomials. For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj52XDLrm
From playlist Rings and modules

Introduction to Witt vectors, delta-rings, and prisms (Lecture 2) by James Borger
PERFECTOID SPACES ORGANIZERS : Debargha Banerjee, Denis Benois, Chitrabhanu Chaudhuri and Narasimha Kumar Cheraku DATE & TIME : 09 September 2019 to 20 September 2019 VENUE : Madhava Lecture Hall, ICTS, Bangalore Scientific committee: Jacques Tilouine (University of Paris, France) Eknat
From playlist Perfectoid Spaces 2019

A Short Course in Algebra and Number Theory - Fields
To supplement a course taught at The University of Queensland's School of Mathematics and Physics I present a very brief summary of algebra and number theory for those students who need to quickly refresh that material or fill in some gaps in their understanding. This is the third lectur
From playlist A Short Course in Algebra and Number Theory

Is it a polynomial with two variables
👉 Learn how to determine whether a given equation is a polynomial or not. A polynomial function or equation is the sum of one or more terms where each term is either a number, or a number times the independent variable raised to a positive integer exponent. A polynomial equation of functio
From playlist Is it a polynomial or not?