
Lecture 11.1 Partial Differential Equations
We introduce Partial Differential Equations (PDEs) and describe how to categorise them. We then discuss two methods that can be used to solve PDEs in certain situations : partial integration and D'Alembert's solution.
From playlist MATH2018 Engineering Mathematics 2D

How to solve the transport equation (PDE)
Free ebook https://bookboon.com/en/partial-differential-equations-ebook How to solve the transport equation, which is an important partial differential equation (PDE) used in modelling. Examples are seen in other videos.
From playlist Partial differential equations
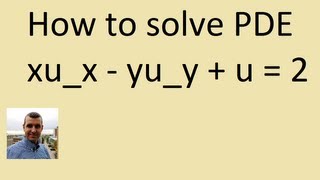
Example of how to solve PDE via change of variables
Free ebook https://bookboon.com/en/partial-differential-equations-ebook An example showing how to solve PDE via change of variables.
From playlist Partial differential equations

An introduction to partial differential equations. PDE playlist: http://www.youtube.com/view_play_list?p=F6061160B55B0203 Part 1 topics: -- what is a partial differential equation -- examples of solutions (4:42) -- ODE versus PDE (10:35)
From playlist Mathematical Physics II - Youtube

Franca Hoffmann: Covariance-modulated optimal transport
HYBRID EVENT Recorded during the meeting " Probability/PDE Interactions: Interface Models and Particle Systems " the April 25, 2022 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by world
From playlist Dynamical Systems and Ordinary Differential Equations

Valeria Simoncini: Computational methods for large-scale matrix equations and application to PDEs
Linear matrix equations such as the Lyapunov and Sylvester equations and their generalizations have classically played an important role in the analysis of dynamical systems, in control theory and in eigenvalue computation. More recently, matrix equations have emerged as a natural linear a
From playlist Numerical Analysis and Scientific Computing

How to solve PDE via directional derivatives
Free ebook https://bookboon.com/en/partial-differential-equations-ebook How to solve PDE via directional derivatives. A basic example is discussed and solved.
From playlist Partial differential equations

Stephan Hoyer: "Improving PDE solvers and PDE-constrained optimization with deep learning and di..."
Machine Learning for Physics and the Physics of Learning 2019 Workshop II: Interpretable Learning in Physical Sciences "Improving PDE solvers and PDE-constrained optimization with deep learning and differentiable programming" Stephan Hoyer - Google Inc. Abstract: Deep learning is differe
From playlist Machine Learning for Physics and the Physics of Learning 2019

Ian Tobasco: "Branching patterns in the optimal design of heat transport"
Transport and Mixing in Complex and Turbulent Flows 2021 "Branching patterns in the optimal design of heat transport" Ian Tobasco - University of Illinois at Chicago, Mathematics Abstract: We consider the related questions of how to (1) optimally transport heat across a fluid layer and (
From playlist Transport and Mixing in Complex and Turbulent Flows 2021

13_2 Optimization with Constraints
Here we use optimization with constraints put on a function whose minima or maxima we are seeking. This has practical value as can be seen by the examples used.
From playlist Advanced Calculus / Multivariable Calculus

DDPS | "When and why physics-informed neural networks fail to train" by Paris Perdikaris
Physics-informed neural networks (PINNs) have lately received great attention thanks to their flexibility in tackling a wide range of forward and inverse problems involving partial differential equations. However, despite their noticeable empirical success, little is known about how such c
From playlist Data-driven Physical Simulations (DDPS) Seminar Series

Steve Brunton - Machine Learning for Scientific Discovery, with Examples in Fluid Mechanics
Recorded 24 January 2023. Steve Brunton of the University of Washington presents "Machine Learning for Scientific Discovery, with Examples in Fluid Mechanics" at IPAM's Learning and Emergence in Molecular Systems Workshop. Abstract: This work describes how machine learning may be used to d
From playlist 2023 Learning and Emergence in Molecular Systems

Ivan Guo: Stochastic Optimal Transport in Financial Mathematics
Abstract: In recent years, the field of optimal transport has attracted the attention of many high-profile mathematicians with a wide range of applications. In this talk we will discuss some of its recent applications in financial mathematics, particularly on the problems of model calibra
From playlist SMRI Seminars

Peng Chen: "Projected Stein variational methods for high-dimensional Bayesian inversion"
High Dimensional Hamilton-Jacobi PDEs 2020 Workshop II: PDE and Inverse Problem Methods in Machine Learning "Projected Stein variational methods for high-dimensional Bayesian inversion constrained by large-scale PDEs" Peng Chen - University of Texas at Austin Abstract: In this talk, I wi
From playlist High Dimensional Hamilton-Jacobi PDEs 2020

Stefan Volkwein: Introduction to PDE-constrained optimization - lecture 2
HYBRID EVENT Recorded during the meeting "Domain Decomposition for Optimal Control Problems" the September 06, 2022 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematici
From playlist Jean-Morlet Chair - Gander/Hubert
Paris Perdikaris: "Overcoming gradient pathologies in constrained neural networks"
Machine Learning for Physics and the Physics of Learning 2019 Workshop III: Validation and Guarantees in Learning Physical Models: from Patterns to Governing Equations to Laws of Nature "Overcoming gradient pathologies in constrained neural networks" Paris Perdikaris - University of Penns
From playlist Machine Learning for Physics and the Physics of Learning 2019

Reinhold Schneider: "Solving Backward Stochastic Differential Equation & HJB equations with Tree..."
Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021 Workshop I: Tensor Methods and their Applications in the Physical and Data Sciences "Solving Backward Stochastic Differential Equation and Hamilton Jacobi Bellmann (HJB) equations with Tree Based Tensor Networ
From playlist Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021
4 Nandakumaran - An Introduction to deterministic optimal control and controllability
PROGRAM NAME :WINTER SCHOOL ON STOCHASTIC ANALYSIS AND CONTROL OF FLUID FLOW DATES Monday 03 Dec, 2012 - Thursday 20 Dec, 2012 VENUE School of Mathematics, Indian Institute of Science Education and Research, Thiruvananthapuram Stochastic analysis and control of fluid flow problems have
From playlist Winter School on Stochastic Analysis and Control of Fluid Flow

How to factor and solve the wave equation (PDE)
Free ebook https://bookboon.com/en/partial-differential-equations-ebook How to solve second order PDE using factoring methods. We solve a range of examples.
From playlist Partial differential equations