
Calculus - The Fundamental Theorem, Part 1
The Fundamental Theorem of Calculus. First video in a short series on the topic. The theorem is stated and two simple examples are worked.
From playlist Calculus - The Fundamental Theorem of Calculus

First Fundamental Theorem of Calculus Calculus 1 AB
I introduce and define the First Fundamental Theorem of Calculus. I finish by working through 4 examples involving Polynomials, Quotients, Radicals, Absolute Value Function, and Trigonometric Functions. Check out http://www.ProfRobBob.com, there you will find my lessons organized by clas
From playlist Calculus

Number Theory - Fundamental Theorem of Arithmetic
Fundamental Theorem of Arithmetic and Proof. Building Block of further mathematics. Very important theorem in number theory and mathematics.
From playlist Proofs

Fundamentals of Mathematics - Lecture 25: Quotient Maps (Real Projective Line, Modular Arithmetic)
course page - https://www.uvm.edu/~tdupuy/logic/Math52-Fall2017.html videography - Eric Melton, UVM
From playlist Fundamentals of Mathematics
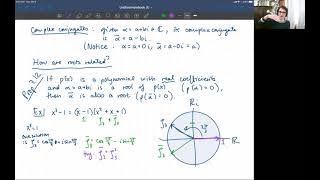
Fundamental Theorem of Algebra
The Fundamental Theorem of Algebra and some additional notes about how roots of polynomials and complex numbers are related to each other.
From playlist Modern Algebra

A group is (in a sense) the simplest structure in which we can do the familiar tasks associated with "algebra." First, in this video, we review the definition of a group.
From playlist Modern Algebra - Chapter 15 (groups)

What is the Fundamental theorem of Algebra, really? | Abstract Algebra Math Foundations 217
Here we give restatements of the Fundamental theorems of Algebra (I) and (II) that we critiqued in our last video, so that they are now at least meaningful and correct statements, at least to the best of our knowledge. The key is to abstain from any prior assumptions about our understandin
From playlist Math Foundations

Abstract Algebra - 11.1 Fundamental Theorem of Finite Abelian Groups
We complete our study of Abstract Algebra in the topic of groups by studying the Fundamental Theorem of Finite Abelian Groups. This tells us that every finite abelian group is a direct product of cyclic groups of prime-power order. Video Chapters: Intro 0:00 Before the Fundamental Theorem
From playlist Abstract Algebra - Entire Course

Fundamentals of Mathematics - Lecture 26: Well-Definedness
course page: https://www.uvm.edu/~tdupuy/logic/Math52-Fall2017.html videography - Eric Melton, UVM
From playlist Fundamentals of Mathematics

Thorben Kastenholz: Simplicial Volume of Total Spaces of Fiber Bundles
Thorben Kastenholz, University of Goettingen Title: Simplicial Volume of Total Spaces of Fiber Bundles It is a classical result that manifolds that are total spaces of fiber bundles, whose fiber has amenable fundamental group, have vanishing simplicial volume. In this talk I will explore t
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022
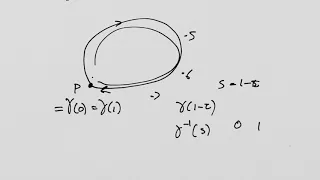
Lie Groups and Lie Algebras: Lesson 35 - The Fundamental Group
Lie Groups and Lie Algebras: Lesson 35 - The Fundamental Group Now that we understand the notion of homotopic paths ina topological space, we focus on loops. Using the fact that homotopy is an equivalence relation we create a set of equivalence classes of homotopic loops. That set is give
From playlist Lie Groups and Lie Algebras

Lucile Vandembroucq (11/19/20): Topological complexity for manifolds with abelian fundamental group
Title: On the nonmaximality of the topological complexity for manifolds with abelian fundamental group Abstract: We will give sufficient conditions for the (normalized) topological complexity of a closed manifold M with abelian fundamental group to be nonmaximal, that is to have TC(M) les
From playlist Topological Complexity Seminar

On Class Number of Number Fields by Debopam Chakraborty
12 December 2016 to 22 December 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore The Birch and Swinnerton-Dyer conjecture is a striking example of conjectures in number theory, specifically in arithmetic geometry, that has abundant numerical evidence but not a complete general solution.
From playlist Theoretical and Computational Aspects of the Birch and Swinnerton-Dyer Conjecture
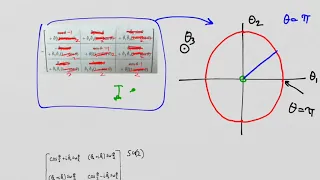
Lie Groups and Lie Algebras: Lesson 37 - The Fundamental Groups of SU(2) and SO(3)
Lie Groups and Lie Algebras: Lesson 37 - Homotopy Groups of SU(2) and SO(3) In this lesson we discover the Fundamental Group of SU(2) and S0(3) and learn the critical fact that they are not the same. That is, the Fundamental Group associated with the topological space SU(2) is simply conn
From playlist Lie Groups and Lie Algebras

Algebraic Topology 1.4 : Fundamental Group
In this video, I introduce the fundamental group, and explain the induced isomorphism resulting from a path and the induced homomorphism resulting from a continuous map, proving functorality. I also briefly cover retractions and how their induced homomorphism is surjective. Translate This
From playlist Topology

What is a Manifold? Lesson 18: Homotopy
What is a Manifold? Lesson 18: Introduction to Homotopy
From playlist What is a Manifold?

Stefan Kebekus The geometry of singularities in the Minimal Model Program and applications to singul
This talk surveys recent results on the singularities of the Minimal Model Program and discusses applications to the study of varieties with trivial canonical class. The first part of the talk discusses an infinitesimal version of the classical decomposition theorem for varieties with vani
From playlist HIM Lectures: Junior Trimester Program "Algebraic Geometry"

Gromov–Witten Invariants and the Virasoro Conjecture - II (Remote Talk) by Ezra Getzler
J-Holomorphic Curves and Gromov-Witten Invariants DATE:25 December 2017 to 04 January 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore Holomorphic curves are a central object of study in complex algebraic geometry. Such curves are meaningful even when the target has an almost complex stru
From playlist J-Holomorphic Curves and Gromov-Witten Invariants

Geometry and topology of Hamiltonian Floer complexes in low-dimension - Dustin Connery-Grigg
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Zoominar Topic: Geometry and topology of Hamiltonian Floer complexes in low-dimension Speaker: Dustin Connery-Grigg Affiliation: Université de Montreal Date: January 28, 2022 In this talk, I will present two results relating
From playlist Mathematics

Definition of a group Lesson 24
In this video we take our first look at the definition of a group. It is basically a set of elements and the operation defined on them. If this set of elements and the operation defined on them obey the properties of closure and associativity, and if one of the elements is the identity el
From playlist Abstract algebra