
Nikos Frantzikinakis: Ergodicity of the Liouville system implies the Chowla conjecture
Abstract: The Chowla conjecture asserts that the signs of the Liouville function are distributed randomly on the integers. Reinterpreted in the language of ergodic theory this conjecture asserts that the Liouville dynamical system is a Bernoulli system. We prove that ergodicity of the Liou
From playlist Jean-Morlet Chair - Lemanczyk/Ferenczi

Learn how to simplify complex fractions. To simplify complex fractions having the addition/subtraction of more than one fractions in the numerator or/and in the denominator we first evaluate the numerator or/and the denominator separately to have one fraction in the numerator and in the de
From playlist How to Simplify Complex Fractions with Trinomials

Alexander Gorodnik - Z^K - actions on nilmanifolds and Diophantine approximation
PROGRAM: RECENT TRENDS IN ERGODIC THEORY AND DYNAMICAL SYSTEMS DATES: Tuesday 18 Dec, 2012 - Saturday 29 Dec, 2012 VENUE: Department of Mathematics,Faculty of Science, The Maharaja Sayajirao University of Baroda, Vadodara PROGRAM LINK: http://www.icts.res.in/program/ETDS2012 DESCR
From playlist Recent Trends in Ergodic Theory and Dynamical Systems

Mixing time-changes of nilflows by Davide Ravotti
PROGRAM SMOOTH AND HOMOGENEOUS DYNAMICS ORGANIZERS: Anish Ghosh, Stefano Luzzatto and Marcelo Viana DATE: 23 September 2019 to 04 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Ergodic theory has its origins in the the work of L. Boltzmann on the kinetic theory of gases.
From playlist Smooth And Homogeneous Dynamics

Simplify a rational expression
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions

Simplify a rational expression
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions (Binomials) #Rational
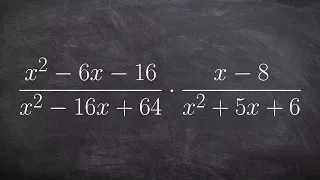
Multiplying two rational expressions with polynomials
Learn how to multiply rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To multiply two rational expressions, we use the distributive property to multiply both numerators togethe
From playlist Multiply Rational Expressions (Trinomials) #Rational

G. Forni - Cohomological equation and Ruelle resonnences (Part 2)
In these lectures we summarized results on the cohomological equation for translation flows on translation surfaces (myself, Marmi, Moussa and Yoccoz, Marmi and Yoccoz) and apply these results to the asymptotic of correlations for pseudo-Anosov maps, which were recently obtained by a direc
From playlist Ecole d'été 2018 - Teichmüller dynamics, mapping class groups and applications

G. Forni - Cohomological equation and Ruelle resonnences (Part 3)
In these lectures we summarized results on the cohomological equation for translation flows on translation surfaces (myself, Marmi, Moussa and Yoccoz, Marmi and Yoccoz) and apply these results to the asymptotic of correlations for pseudo-Anosov maps, which were recently obtained by a direc
From playlist Ecole d'été 2018 - Teichmüller dynamics, mapping class groups and applications

G. Forni - Cohomological equation and Ruelle resonnences (Part 1)
In these lectures we summarized results on the cohomological equation for translation flows on translation surfaces (myself, Marmi, Moussa and Yoccoz, Marmi and Yoccoz) and apply these results to the asymptotic of correlations for pseudo-Anosov maps, which were recently obtained by a direc
From playlist Ecole d'été 2018 - Teichmüller dynamics, mapping class groups and applications

Federico Rodriguez Hertz: Rigidity of hyperbolic higher rank lattice actions
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Dynamical Systems and Ordinary Differential Equations

Almost all dynamically syndetic sets are multiplicatively thick - Daniel Glasscock
Special Year Research Seminar Topic: Almost all dynamically syndetic sets are multiplicatively thick Speaker: Daniel Glasscock Affiliation: University of Massachusetts Lowell Date: November 22, 2022 If a set of integers is syndetic (finitely many translates cover the integers), must it c
From playlist Mathematics

Learn how to simplify complex fractions. To simplify complex fractions having the addition/subtraction of more than one fractions in the numerator or/and in the denominator we first evaluate the numerator or/and the denominator separately to have one fraction in the numerator and in the de
From playlist How to Simplify Complex Fractions with Trinomials

Simplify a rational expression
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions (Binomials) #Rational

Linear Equations in Primes and Nilpotent Groups - Tamar Ziegler
Tamar Ziegler Technion--Israel Institute of Technology January 30, 2011 A classical theorem of Dirichlet establishes the existence of infinitely many primes in arithmetic progressions, so long as there are no local obstructions. In 2006 Green and Tao set up a program for proving a vast gen
From playlist Mathematics
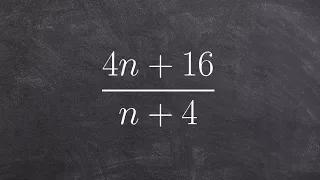
Simplifying rational expression
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions (Binomials) #Rational

Math tutorial for simplifying complex fractions
👉 Learn how to simplify complex fractions. To simplify complex fractions having the addition/subtraction of more than one fractions in the numerator or/and in the denominator we first evaluate the numerator or/and the denominator separately to have one fraction in the numerator and in the
From playlist How to Simplify Complex Fractions with Monomials
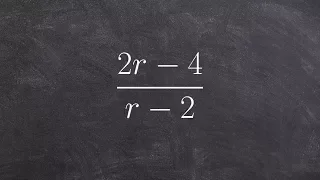
Simplifying a rational expression by factoring out the numerator
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions (Binomials) #Rational

Corinna Ulcigrai - 5/6 Parabolic dynamics and renormalization: an introduction
Parabolic dynamical systems are mathematical models of the many phenomena which display a "slow" form of chaotic evolution, in the sense that nearby trajectories diverge polynomially in time. In contrast with hyperbolic and elliptic dynamical systems, there is no general theory which desc
From playlist Corinna Ulcigrai - Parabolic dynamics and renormalization: an introduction

👉 Learn how to simplify complex fractions. To simplify complex fractions having a fraction as the numerator and another fraction as the denominator we first factor the expressions that can be factored and then we multiply the fraction in the numerator with the reciprocal of the fraction in
From playlist Simplify Complex Fractions 2 Terms | 5 Examples